Cho hình hộp chữ nhật $\large ABCD.A'B'C'D'$ có độ dài đường chéo $\la

Cho hình hộp chữ nhật $\large ABCD.A'B'C'D'$ có độ dài đường chéo $\large AC'=\sqrt{18}$. Gọi $\large S$ là diện tích toàn phần của hình hộp chữ nhật đã cho. Tìm giá trị lớn nhất $\large S_{max}$ của $\large S$

• A.

  A. $\large S_{max}=18$

• B.

  B. $\large S_{max}=18\sqrt{3}$

• C.

  C. $\large S_{max}=36$

• D.

  D. $\large S_{max}=36\sqrt{3}$

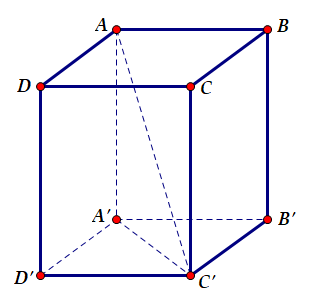
Gọi $\large a,b,c$ là ba kích thước của hình hộp chữ nhật. 

Khi đó $\large S_{tp}=2(ab+bc+ca)$

Theo giả thiết ta có $\large a^{2}+b^{2}+c^{2}=AC'^{2}=18$

Từ bất đẳng thức $\large a^{2}+b^{2}+c^{2}\geq ab+bc+ca$, suy ra $\large S_{tp}=2(ab+bc+ca)\leq 2\cdot 18=36$

Dấu "=" xảy ra $\large\Leftrightarrow a=b=c=\sqrt{6}$

Đáp án C