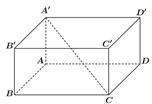
Cho hình hộp chữ nhật $\Large ABCD.{A}'{B}'{C}'{D}'$, có $\Large AB=A{

Cho hình hộp chữ nhật $\Large ABCD.{A}'{B}'{C}'{D}'$, có $\Large AB=A{A}'=a$, $\Large AD=a\sqrt{2}$ (tham khảo hình vẽ). Góc giữa đường thẳng $\Large {A}'C$ và mặt phẳng $\Large \left( ABCD \right)$ bằng

• A. $\Large {{30}^{\circ }}$.
• B. $\Large {{45}^{\circ }}$.
• C. $\Large {{90}^{\circ }}$.
• D. $\Large {{60}^{\circ }}$.

Chọn A

Vì $\Large ABCD$ là hình chữ nhật, có $\Large AB=a$, $\Large AD=a\sqrt{2}$ nên

$\Large AC=BD=\sqrt{A{{B}^{2}}+A{{D}^{2}}}=\sqrt{{{a}^{2}}+{{\left( a\sqrt{2} \right)}^{2}}}=a\sqrt{3}$

Ta có $\Large \left( {A}'C;\left( ABCD \right) \right)=\left( {A}'C;CA \right)=\widehat{{A}'CA}$

Do tam giác $\Large {A}'AC$ vuông tại $\Large A$ nên $\Large \tan \widehat{{A}'AC}=\dfrac{A{A}'}{AC}=\dfrac{a}{a\sqrt{3}}=\dfrac{1}{\sqrt{3}}$ $\Large \Rightarrow $ $\Large \widehat{{A}'AC}={{30}^{\circ }}$.