Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=a, AC=a√3; SA vuông góc với đáy, SA=2a. Khoảng cách từ điểm A đến mặt phẳng (SBC) bằng
Đáp án án đúng là: D
Lời giải chi tiết:
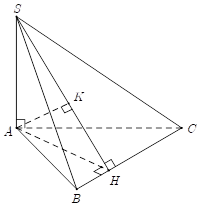
Ta có SA⊥(ABC)BC⊂(ABC)}⇒SA⊥BC.
Trong (ABC), kẻ AH⊥BC, mà BC⊥SA⇒BC⊥(SAH)⇒BC⊥SH.
Trong (SAH), kẻ AK⊥SH, mà SH⊥BC ⇒AK⊥(SBC) hay d(A;(SBC))=AK.
Vì ΔABC vuông tại Anên BC=√AB2+AC2=2a.
Mặt khác có AH là đường cao nên AH=AB.ACBC=√3a2.
Vì ΔSAH vuông tại A nên SH=√SA2+AH2=√19a2.
Vậy có AK là đường cao AK=SA.AHSH=2a√3√19.
Nhận xét. Trong thực hành làm toán trắc nghiệm ta nên áp dụng bài toán sau:
Cho tứ diện OABC có OA,OB,OCđôi một vuông góc với nhau và H là hình chiếu của O lên mặt phẳng (ABC). Khi đó 1OH2=1OA2+1OB2+1OC2.
Xem thêm các bài tiếp theo bên dưới