Cho hàm số $\Large y=f(x)$ có đạo hàm liên tục trên $\Large \left( -1;

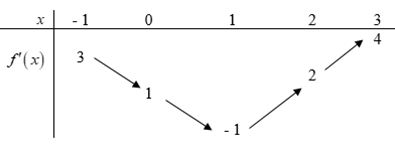
Cho hàm số $\Large y=f(x)$ có đạo hàm liên tục trên $\Large \left( -1;\,3 \right)$. Bảng biến thiên của hàm số $\Large y={f}'\left( x \right)$ được cho như hình vẽ sau. Hàm số $\Large y=f\left( 1-\dfrac{x}{2} \right)+x$ nghịch biến trên khoảng nào sau đây?

• A. $\Large \left( -4;-2 \right)$.
• B. $\Large \left( -2;0 \right)$.
• C. $\Large \left( 0;2 \right)$.
• D. $\Large \left( 2;4 \right)$.

Chọn A

Xét hàm số: $\Large y=f\left( 1-\dfrac{x}{2} \right)+x$.

Ta có: $\Large {y}'={f}'\left( 1-\dfrac{x}{2} \right).\left( -\dfrac{1}{2} \right)+1$.

Hàm số $\Large y=f\left( 1-\dfrac{x}{2} \right)+x$ nghịch biến khi $\Large {f}'\left( 1-\dfrac{x}{2} \right)\ge 2\,\,\,\left( * \right)$

Từ bảng biến thiên ta có:

$\Large \left( * \right)\Rightarrow \left[ \begin{matrix}& 2\le 1-\dfrac{x}{2}\le 3\Leftrightarrow -4\le x\le -2. \\ & a\le 1-\dfrac{x}{2}\le -1\,\,\,\,\,\left( -1

Trong các đáp án ta chỉ có thể chọn đáp án $\Large A$.