Cho hình hộp chữ nhật $\Large ABCD.A'B'C'D'$ có đáy $\Large ABCD$ là h

Cho hình hộp chữ nhật $\Large ABCD.A'B'C'D'$ có đáy $\Large ABCD$ là hình vuông cạnh $\Large 2\sqrt{2}$, $\Large AA'=4$. Tính góc giữa đường thẳng $\Large A'C$ với mặt phẳng $\Large (AA'B'B)$.

• A.

  $\Large 60^{\circ}$.

• B.

  $\Large 45^{\circ}$.

• C.

  $\Large 90^{\circ}$.

• D.

  $\Large 30^{\circ}$.

Chọn D

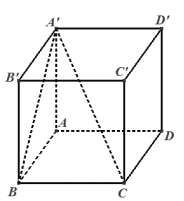
Ta có $\Large CB\perp AB$, $\Large CB\perp BB'$ $\Large \Rightarrow CB\perp (AA'B'B)$.

$\Large \Rightarrow A'C$ có hình chiếu là $\Large A'B$ trên $\Large (AA'B'B)$ $\Large \Rightarrow \big(A'C, (AA'B'B)\big)=(A'C, A'B)=\widehat{CA'B}$ (vì $\Large \Delta CA'B$ vuông tại $\Large B$ nên $\Large \widehat{CA'B}$ nhọn).

Ta có $\Large A'B=\sqrt{AA'^2+AB^2}=2\sqrt{6}$ $\Large \Rightarrow tan\widehat{CA'B}=\dfrac{BC}{A'B}=\dfrac{1}{\sqrt{3}}$ $\Large \Rightarrow \widehat{CA'B}=30^{\circ}$.