Cho hàm số $\Large y=f(x)$ có đạo hàm $\Large f'(x)=3x^2+6x+4$, $\Larg

Cho hàm số $\Large y=f(x)$ có đạo hàm $\Large f'(x)=3x^2+6x+4$, $\Large \forall x\in \mathbb{R}$. Có tất cả bao nhiêu giá trị nguyên thuộc (-2020; 2020) của tham số $\Large m$ để hàm số $\Large g(x)=f(x)-(2m+4)x-5$ nghịch biến trên (0; 2)?

• A. 2008.
• B. 2007.
• C. 2018.
• D. 2019.

Chọn A
Ta có $\Large g'(x)=f'(x)-(2m+4)$.

Hàm số $\Large g(x)=f(x)-(2m+4)x-5$ nghịch biến trên (0; 2) khi $\Large g'(x)\leq 0$, $\Large \forall x\in (0; 2)$

$\Large \Leftrightarrow f'(x)-(2m+4)\leq 0$, $\Large \forall x\in (0; 2)$ $\Large \Leftrightarrow 3x^2+6x+4\leq 2m+4$, $\Large \forall x\in (0; 2)$

Xét hàm số $\Large h(x)=3x^2+6x+4$ $\Large \Rightarrow h'(x)=6x+6$. Ta có BBT:

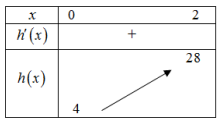
Vậy $\Large 2m+4\geq 28$ $\Large \Leftrightarrow m\geq 12$. Vì $\Large m$ nguyên thuộc (-2020; 2020) nên có 2008 giá trị thỏa mãn.