Gọi $\Large S$ là tập tất cả các giá trị của tham số $\Large m$ để đồ

Gọi $\Large S$ là tập tất cả các giá trị của tham số $\Large m$ để đồ thị hàm số $\Large y=x^3+3x^2-9x+2m+1$ và trục $\Large Ox$ có đúng hai điểm chung phân biệt. Tính tổng $\Large T$ của các phần tử thuộc tập $\Large S$.

• A.

  $\Large T=-10$.

• B.

  $\Large T=10$.

• C.

  $\Large T=-12$.

• D.

  $\Large T=12$.

Chọn C
Hoành độ giao điểm của đồ thị hàm số $\Large y=x^3+3x^2-9x+2m+1$ và trục $\Large Ox$ là nghiệm của phương trình: $\Large x^3+3x^2-9x+2m+1=0$ $\Large \Leftrightarrow -x^3-3x^2+9x=2m+1$.

Xét hàm số $\Large f(x)=-x^3-3x^2+9x$.

Tập xác định: $\Large D=\mathbb{R}$.

$\Large f'(x)=-3x^2-6x+9$, $\Large f'(x)=0$ $\Large \Leftrightarrow -3x^2-6x+9=0$ $\Large \Leftrightarrow \left[\begin{align} & x=1 \\ & x=-3 \end{align}\right.$.

Bảng biến thiên:

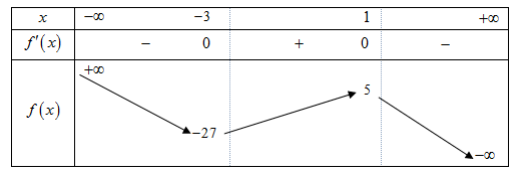Đồ thị hàm số $\Large y=x^3+3x^2-9x+2m+1$ cắt trục $\Large Ox$ tại hai điểm phân biệt khi và chỉ khi đường thẳng $\Large y=2m+$ cắt đồ thị hàm số $\Large f(x)=-x^3-3x^2+9x$ tại hai điểm phân biệt.

Từ bảng biến thiên suy ra: $\Large \left[\begin{align} & 2m+1=5 \\ & 2m+1=-27 \end{align}\right.$ $\Large \Leftrightarrow \left[\begin{align} & m=2 \\ & m=-14 \end{align}\right.$ $\Large \Rightarrow S=\begin{Bmatrix} -14; 2 \end{Bmatrix}$.

Tổng của các phần tử thuộc tập $\Large S$ là: $\Large T=-14+2=-12$.