Cho hình hộp ABCD.A'B'C'D' có thể tích V. Một mặt phẳng (Q) đi qua trọ

Cho hình hộp ABCD.A'B'C'D' có thể tích V. Một mặt phẳng (Q) đi qua trọng tâm của tam giác ABD và trung điểm CC' đồng thời (Q) song song với BD. Mặt phẳng (Q) chia khối hộp ABCD.A'B'C'D' thành hai phần. Thể tích của phần chứa A' bằng

• A.

  $\Large \dfrac{181}{216}V.$

• B.

  $\Large \dfrac{187}{216}V.$

• C.

  $\Large \dfrac{185}{216}V.$

• D.

  $\Large \dfrac{191}{216}V.$

Chọn C

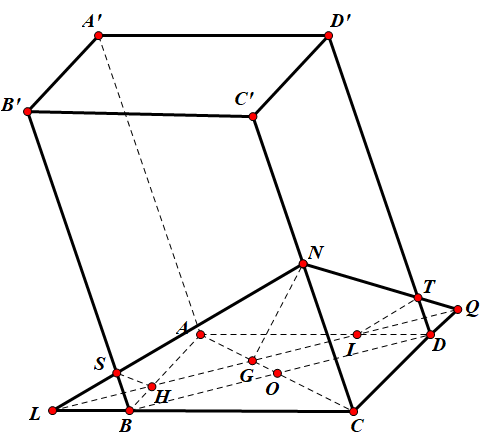
Ta có:

$\Large \Rightarrow S_{\Delta AIH}=\dfrac{1}{2}.AH.AI=\dfrac{1}{2}.\dfrac{2}{3}AB.\dfrac{2}{3}AC=\dfrac{2}{9}.AB.AC=\dfrac{2}{9}S_{ABCD}$

$\Large S_{\Delta IDQ}=S_{\Delta HBL}=\dfrac{1}{4}S_{\Delta AHI}=\dfrac{1}{18}S_{ABCD}.$

Ta có $\Large {S_{BCDIH}} = {S_{ABCD}} - {S_{AIH}} = { S_{ABCD}} - \dfrac{2}{9}{S  _{ABCD}} = \dfrac{7}{9}{ S _{ABCD}}$

Gọi h là chiều cao của hình hộp.

Ta có $\Large V_{N.CLQ}=\dfrac{1}{3}.\dfrac{h}{2}.S_{CLQ}$ $\Large =\dfrac{h}{6}.(S_{BCDIH}+2S_{\Delta HBL})$ $\Large =\dfrac{h}{6}\left(\dfrac{7}{9}S_{ABCD}+2\dfrac{1}{18}S_{ABCD}\right)=\dfrac{4}{27}V$

$\Large V_{S.LBH}=\dfrac{1}{3}d\big(S, (ABCD)\big).S_{\Delta HBL}$ $\Large =\dfrac{1}{3}.\dfrac{LS}{LN}d\big(N, (ABCD)\big).\dfrac{1}{18}S_{ABCD}$ $\Large =\dfrac{1}{3}.\dfrac{1}{4}.\dfrac{h}{2}.\dfrac{1}{18}S_{ABCD}$ $\Large =\dfrac{1}{432}h.S_{ABCD}=\dfrac{V}{432}$

Suy ra $\Large V_1=V-(V_{N.CLQ}-2V_{S.HBL})$ $\Large =V-\left(\dfrac{4}{27}V-2\dfrac{V}{432}\right)=\dfrac{185}{216}V.$