Cho khối trụ có chiều cao 20cm. Cắt khối trụ bởi một mặt phẳng được th

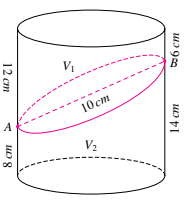
Cho khối trụ có chiều cao 20cm. Cắt khối trụ bởi một mặt phẳng được thiết diện là hình elip có độ dài trục lớn bằng 10cm. Thiết diện chia khối trụ ban đầu thành hai nửa, nửa trên có thể tích $\Large V_1,$ nửa dưới có thể tích $\Large V_2$ (như hình vẽ). Khoảng cách từ một điểm thuộc thiết diện gần đáy dưới nhất và điểm thuộc thiết diện xa đáy dưới nhất tới đáy dưới là 8cm và 14cm. Tính tỉ số $\Large \dfrac{V_1}{V_2}.$

• A.

  $\Large \dfrac{6}{11}.$

• B.

  $\Large \dfrac{9}{20}.$

• C.

  $\Large \dfrac{11}{20}.$

• D.

  $\Large \dfrac{9}{11}.$

Chọn D

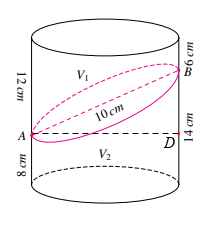
$\Large V_2=\pi R^2\left(\dfrac{h_1+h_2}{2}\right)=\pi R^2\left(\dfrac{8+14}{2}\right)=11\pi R^2.$

$\Large \Delta ABD$ vuông tại D có $\Large 2R=AD=\sqrt{AB^2-BD^2}=\sqrt{10^2-(14-8)^2}=8 \Rightarrow R=4.$

$\Large V=\pi r^2.h=320\pi$

$\Large V_2=\pi 4^2.11=176\pi$

$\Large V_1=V-V_2=144\pi \Rightarrow \dfrac{V_1}{V_2}=\dfrac{9}{11}$