Trong không gian $\Large Oxyz$, cho $\Large A(3; 0; 0), B(0; 3; 0), C(

Trong không gian $\Large Oxyz$, cho $\Large A(3; 0; 0), B(0; 3; 0), C(0; 0; 3)$. Gọi $\Large (P)$ là mặt phẳng chứa cạnh $\Large AB$ và vuông góc với $\Large (ABC)$. $\Large (C)$ là đường tròn đường kính $\Large AB$ và nằm trong mặt phẳng $\Large (P)$. Gọi $\Large S$ là một điểm bất kỳ nằm trên $\Large (C)$, $\Large S$ khác $\Large A, B$. Khi đó khoảng cách từ tâm mặt cầu ngoại tiếp tứ diện $\Large S.ABC$ đến mặt phẳng $\Large (Q): 2x+3y+z+1=0$ bằng

• A. $\Large \dfrac{7}{\sqrt{14}}$.
• B. $\Large \dfrac{3}{2\sqrt{14}}$.
• C. $\Large \dfrac{6}{\sqrt{14}}$.
• D. $\Large \dfrac{3}{\sqrt{14}}$.

Chọn A

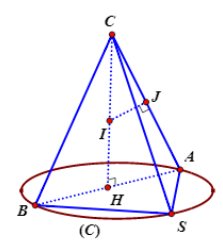
Dễ thấy tâm mặt cầu ngoại tiếp tứ diện $\Large S.ABC$ không phụ thuộc vị trí điểm $\Large S$.

Gọi $\Large H\left(\dfrac{3}{2}; \dfrac{3}{2}; 0\right)$ là trung điểm $\Large AB$. Suy ra $\Large H$ là tâm của $\Large (C)$ và $\Large CH\perp AB$ $\Large \Rightarrow CH\perp (SAB)$ hay $\Large CH$ là trục của đường tròn $\Large (C)$. Có $\Large \overrightarrow{CH}=\left(\dfrac{3}{2}; \dfrac{3}{2}; -3\right)=\dfrac{3}{2}(1; 1; -2)$ suy ra $\Large CH$ có phương trình $\Large x=t; y=t; z=3-2t$.

Mặt phẳng trung trực đoạn $\Large AC$ đi qua trung điểm $\Large J\left(\dfrac{3}{2}; 0; \dfrac{3}{2}\right)$ của $\Large AC$ và có VTPT là $\Large \overrightarrow{AC}=(-3; 0; 3)=-3(1; 0; -1)$ nên có phương trình: $\Large \left(x-\dfrac{3}{2}\right)-\left(z-\dfrac{3}{2}\right)=0$ hay $\Large (\alpha): x-z=0$.

Suy ra tâm của mặt cầu ngoại tiếp tứ diện $\Large S.ABC$ là giao điểm $\Large I$ của $\Large CH$ và $\Large (\alpha)$, tìm được $\Large I(1; 1; 1)$. Do đó $\Large d(I, (Q))=\dfrac{|2+3+1+1|}{\sqrt{4+9+1}}=\dfrac{7}{\sqrt{14}}$.