Xét các số phức $\Large z$ thỏa mãn $\Large |z+\overline{z}|+|z-\overl

Xét các số phức $\Large z$ thỏa mãn $\Large |z+\overline{z}|+|z-\overline{z}|=|z|^2$. Tìm giá trị lớn nhất của $\Large |z-4+3i|$.

• A.

  $\Large \sqrt{41}+\sqrt{2}$.

• B.

  $\Large \sqrt{41}-\sqrt{2}$.

• C.

  $\Large \sqrt{5}+2$.

• D.

  $\Large \sqrt{29}+\sqrt{2}$.

Đặt $\Large z=x+yi; x, y\in\mathbb{R}$. Giả thiết trở thành

$\Large 2|x|+2|y|=x^2+y^2$ $\Large \Leftrightarrow (|x|-1)^2+(|y|-1)^2=2$ (1)

• Với $\Large x\geq 0, y\geq 0$ thì phương trình (1) trở thành $\Large (x-1)^2+(y-1)^2=2$ (2)

Các điểm $\Large M(x; y)$ thỏa mãn (2) nằm trên đường tròn tâm $\Large A(1; 1)$ bán kính $\Large r=\sqrt{2}$.

Do đó, các điểm $\Large M(x; y)$ thỏa mãn (1) trong trường hợp này là phần đường tròn $\Large (A; \sqrt{2})$ ở góc phần tư thứ (I), bao gồm cả điểm $\Large O$. Kí hiệu tập hợp các điểm này là $\Large (l)$.

• Nhận xét rằng, nếu $\Large (x; y)$ là nghiệm của (1) thì $\Large (-x; y), (x; -y), (-x; -y)$ cũng là nghiệm của (1), nên tập hợp các điểm thỏa mãn (1) đối xứng qua hai trục tọa độ và qua $\Large O$.

Do đó, bằng cách lấy đối xứng của $\Large (l)$ qua các trục tọa độ và qua $\Large O$ ta được tập hợp các điểm $\Large M$ là đường cong $\Large (H)$ kể cả gốc tọa độ $\Large O$. Đường cong $\Large (H)$ là các cung tròn của các đường tròn $\Large (A; \sqrt{2}), (B; \sqrt{2}), (C; \sqrt{2}), (D; \sqrt{2})$ với $\Large A(1; 1), B(1; -1), C(-1; -1), D(-1; 1)$ (như hình vẽ dưới đây).

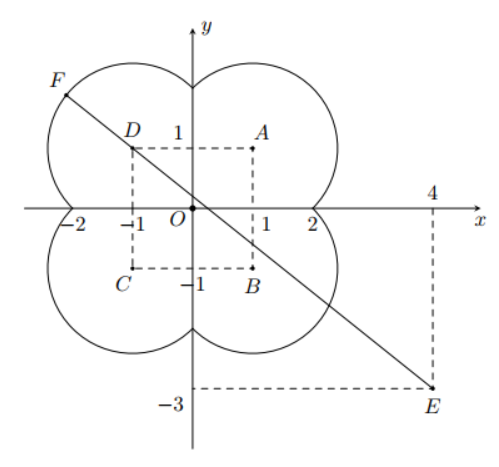
Gọi $\Large E(4; -3)$ suy ra $\Large |z-4+3i|=ME$.

Dễ thấy khi đó giá trị lớn nhất của $\Large ME=ED+R=\sqrt{41}+\sqrt{2}$.

Chọn đáp án A