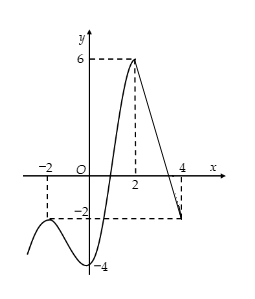
Cho hàm số $\Large y=f(x)$ có đồ thị như hình vẽ bên. Có bao nhiêu số

Cho hàm số $\Large y=f(x)$ có đồ thị như hình vẽ bên.

Có bao nhiêu số nguyên của tham số m để phương trình $\Large \dfrac{1}{3}f\left(\dfrac{x}{2}+1\right)+x=m$ có nghiệm thuộc [-2; 2]?

• A. 7.
• B. 6.
• C. 8.
• D. 5.

Chọn C

Đặt $\Large t=\dfrac{x}{2}+1$ ta có:

Vì $\Large x \in [-2; 2] \Rightarrow t \in [0; 2]$

Và $\Large \dfrac{1}{3}f(t)+2(t-1)=m.$

Xét hàm $\Large g(t)=\dfrac{1}{3}f(t)+2(t-1)$ trên đoạn [0; 2]:

$\Large {g}'(t)=\dfrac{1}{3}{f}'(t)+2=\dfrac{{f}'(t)+6}{3} > 0 ,\forall t \in [0; 2]$

Như vậy hàm $\Large g(t)=\dfrac{1}{3}f(t)+2(t-1)$ là hàm đồng biến trên [0; 2]

Để phương trình ban đầu có nghiệm $\Large x \in [-2; 2]$ thì phương trình có nghiệm $\Large t \in [0; 2].$

Khi đó:

$\Large \underset{[0; 2]}{\min}g(t) \leq m \leq \underset{[0; 2]}{\max}g(t)$

$\Large \Leftrightarrow g(0) \leq m \leq g(2)$

$\Large \Leftrightarrow \dfrac{1}{3}f(0) + 2(0-1) \leq m \leq \dfrac{1}{3}f(2)+2(2-1)$

$\Large \Leftrightarrow \dfrac{1}{3}(-4)-2 \leq m \leq \dfrac{1}{3}.6+2$

$\Large \Leftrightarrow \dfrac{-10}{3} \leq m \leq 4$

Vì $\Large m \in Z$ nên $\Large m \in \begin{Bmatrix} -3; -2; -1; 0; 1; 2; 3; 4 \end{Bmatrix}.$

Vậy có tất cả 8 giá trị nguyên m thỏa mãn yêu cầu bài toán.