Cho hình chóp tứ giác đều S.ABCD có tất cả cách cạnh bằng a. Gọi M là

Cho hình chóp tứ giác đều S.ABCD có tất cả cách cạnh bằng a. Gọi M là trung điểm của SD (tham khỏa hình vẽ bên). Tang của góc giữa đường thẳng BM và mặt phẳng (ABCD) bằng: 

• A. A. $\large \dfrac{\sqrt{2}}{2}$
• B. B. $\large \dfrac{\sqrt{3}}{3}$
• C. C. $\large \dfrac{2}{3}$
• D. D. $\large \dfrac{1}{3}$

Chọn D

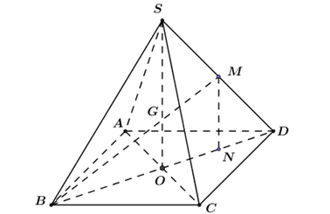
Gọi G là giao điểm của BM và SO
Từ M kẻ đường thẳng vuông góc với BD tại N. Khi đó ta có: $\large MN//SO\Rightarrow MN\perp (ABCD)$
$\large \Rightarrow $ N là hình chiếu của M trên (ABCD)
$\large \Rightarrow \angle (BM, (ABCD))= \angle (BM, BD)= \widehat{MBD}$ 
Xét tam giác SBD có MB và BD là hai đường trung tuyến cắt nhau tại G $\large \Rightarrow $ G là trọng tâm tam giác SBD $\large \Rightarrow OG= \dfrac{1}{3}SO$
Ta có: $\large BO = \dfrac{1}{2}BD= \dfrac{a\sqrt{2}}[2}\Rightarrow S= \sqrt{SB^2- OB^2}= \sqrt{a^2- \dfrac{a^2}{2}}= \dfrac{a\sqrt{2}}{2}\Rightarrow OG= \dfrac{a\sqrt{2}}{6}$
$\large \tan \widehat{MBD}= \dfrac{OG}{OB}= \dfrac{a\sqrt{2}}{6}. \dfrac{2}{a\sqrt{2}}= \dfrac{1}{3}$