Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với (ABCD). Tính khoảng cách giữa hai đường thẳng chéo nhau SA và BC

• A. A. $\large \dfrac{a\sqrt{3}}{2}$
• B. B. $\large a$
• C. C. $\large \dfrac{a\sqrt{3}}{4}$
• D. D. $\large \dfrac{a}{2}$

Chọn A

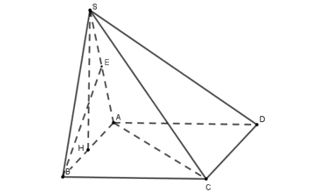
Vì tam giác đều và nằm trong mặt phẳng vuông góc với đáy nên lấy H là trung điểm của AB. Khi đó, ta có: $\large \left\{\begin{align}& (SAB)\perp (ABCD)\\& (SAB)\cap (ABCD)= AB\\& SH\perp AB\\\end{align} \right.$ $\large \Rightarrow SH\perp (ABCD)$
Gọi E là trung điểm SA thì tam giác SAB đều nên $\large BE\perp SA$
Ta có: $\large \left\{\begin{align}& BC\perp AB\\& BC\perp SH\\\end{align} \right.$ $\large \Rightarrow BC\perp (SAB)\Rightarrow BC\perp BE$ mà $\large BE\perp SA$ nên BE là đoạn vuông góc chung của SA và BC
Từ đó $\large d(SA, BC) = BE$
Vì $\large AB= a$ nên tam giác SAB đều cạnh a $\large \Rightarrow BE= \dfrac{a\sqrt{3}}{2}\Rightarrow d(SA, BC) = \dfrac{a\sqrt{3}}{2}$