Cho hình chóp S. ABCD có đáy là hình vuông ABCD cạnh a, SA vuông góc v

Cho hình chóp S. ABCD có đáy là hình vuông ABCD cạnh a, SA vuông góc với mặt phẳng đáy. Tính độ dài của SA để hai mặt phẳng (SBC) và (SCD) tạo với nhau góc $\large 60^\circ $

• A. A. $\large a$
• B. B. $\large \dfrac{a}{2}$
• C. C. $\large \dfrac{a\sqrt{3}}{2}$
• D. D. $\large a\sqrt{2}$

Chọn A

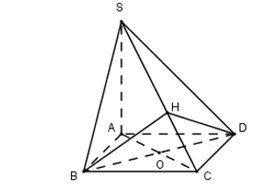
Ta có: $\large \left\{\begin{align}& BD\perp SA\\& BS\perp AC\\\end{align} \right.$ $\large \Rightarrow BD\perp (SAC)\Rightarrow BD\perp SC$
Trong (SBC) kẻ $\large BH\perp SC\Rightarrow SC\perp (BDH)\Rightarrow DH\perp SC$
Ta có: $\large \left\{\begin{align}& (SBC)\cap (SCD)= SC\\& (SBC)\supset BH\perp SC\\& (SCD)\supset DH\perp SC\\\end{align} \right.$ $\large \Rightarrow \angle ((SBC), (SCD))= \angle (BH, DH)= 60^\circ $ $\large \Rightarrow \left[ \begin(align}& \widehat {BHD}= 60^\circ \\& \widehat{BHD}= 120^\circ \\\end{align}\right.$
Có: $\large \left\{\begin{align}& BC\perp AB\\& BC\perp SA\\\end{align} \right.$ $\large \Rightarrow BC\perp (SAB)\Rightarrow BC\perp SB\Rightarrow \Delta SBC$ vuông tại B, tương tự ta có CM được tam giác SCD vuông tại D
Dễ thấy: $\large \Delta SAB= \Delta SAD$ (c.g.c) $\large \Rightarrow SB= SD\Rightarrow \Delta SBC= \Delta SDC$ (c.c.c)
$\large \Rightarrow BH= DH\Rightarrow \Delta BDH$ cân tại H
Đặt $\large SA= x$, ta có: $\large SB= \sqrt{x^2+ a^2}\Rightarrow BH^2= \dfrac{SB^2.BC^2}{SB^2+BC^2}= \dfrac{(x^2+a^2). A^2}{x^2+ 2a^2}= DH^2$, ABCD là hình vuông cạnh a
$\large \Rightarrow BD=a\sqrt{2}\Rightarrow BO= \dfrac{a\sqrt{2}}{2}$
TH1: $\large \widehat{BHD}= 60^\circ \Rightarrow \widehat{BHO}= 30^\circ $, xét tam giác vuông BHO có: 
$\large \dfrac{BO}{BH}= \sin 30^\circ = \dfrac{1}{2}\Leftrightarrow \dfrac{BO^2}{BH^2}= \dfrac{1}{4}$
$\large \Leftrightarrow \dfrac{\dfrac{a^2}{2}}{\dfrac{(x^2+a^2)a^2}{x^2+2a^2}}= \dfrac{1}{4}\Leftrightarrow \dfrac{x^2+a^2}{x^2+2a^2}= 2\Leftrightarrow x^2+a^2= 2x^2+ 4a^2\Leftrightarrow x^2= -3a^2$ (vô lý)
TH2: $\large \widehat{BHD}= 120^\circ\Rightarrow \widehat{BHO] = 60^\circ  $, xét tam giác vuông BHO có: 
$\large \dfrac{BO}{BH}= \sin 60^\circ = \dfrac{\sqrt{3}}{2}\Leftrightarrow \dfrac{BO^2}{BH^2}= \dfrac{3}{4}$ 
$\large \Leftrightarrow \dfrac{\dfrac{a^2}{2}}{\dfrac{(x^2+a^2)a^2}{x^2+2a^2}}= \dfrac{3}{4}\Leftrightarrow \dfrac{x^2+a^2}{x^2+2a^2}= \dfrac{2}{3}\Leftrightarrow 3x^2+3a^2= 2x^2+ 4a^2\Leftrightarrow x^2= a^2\Leftrightarrow x= a$