Cho hình chóp S.ABC có đáy là tam giác đều cạnh $\large a= 4\sqrt{2}\,

Cho hình chóp S.ABC có đáy là tam giác đều cạnh $\large a= 4\sqrt{2}\, cm $, cạnh bên SC vuông góc với đáy và $\large SC= 2\, cm$. Gọi M, N là trung điểm của AB và BC.Góc giữa hai đường thẳng SN và CM là: 

• A. A. $\large 45^\circ $
• B. B. $\large 60^\circ $
• C. C. $\large 90^\circ $
• D. D. $\large 30^\circ $

Chọn A

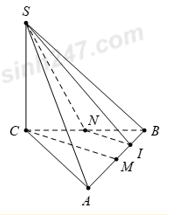
Gọi I là trung điểm của BM $\large \Rightarrow CM//NI$
$\large \Rightarrow \angle (SN, CM)= $ $\large \left[\begin{align}& \widehat SNI\, \text{khi}\, 0^\circ  < \widehat{SNI} < 90^\circ \\& 180^\circ -\widehat{SNI}\, \text{khi}\, 90^\circ < \widehat{SNI} < 180^\circ $ 
Tam giác SCN vuông tại C, có $\large SN=\sqrt{SC^2+ CN^2}= 2\sqrt{3}\, cm$
Tam giác ABC đều $\large \Rightarrow CM= 2\sqrt{6}\, cm\Rightarrow NI = \sqrt{6}\, cm$
Tam giác SCM vuông tại C, có $\large SM= \sqrt{SC^2+ CM^2}= 2\sqrt{7}\, cm$
$\large \Rightarrow SI= \sqrt{SM^2+ MI^2}= \sqrt{SM^2+ \left( \dfrac{AB}{4}\right)^2}}= \sqrt{\left( 2\sqrt{7}\right)^2+ \left( \dfrac{4\sqrt{2}}{4}\right)^2}= \sqrt{30}\, cm$
Khi đó: $\large \co \widehat{SNI}= \dfrac{SN^2+ NI^2- SI^2}{2.SN.NI]= - \dfrac{\sqrt{2}}{2}\Rightarrow \widehat{SNI}= 135^\circ $
Vậy $\large \angle (SN, CM) = 45^\circ $