Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 1, cạnh bên hợp với

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 1, cạnh bên hợp với mặt đáy một góc $\large 60^\circ $. Tính khoảng cách d từ O đến mặt phẳng (SBC)

• A. $\large d= \dfrac{1}{2}$
• B. $\large d= \dfrac{\sqrt{2}}{2}$
• C. $\large d= \dfrac{\sqrt{7}}{2}$
• D. $\large d= \dfrac{\sqrt{42}}{14}$

Chọn D

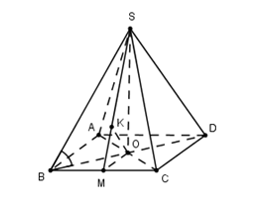
Gọi O là tâm hình vuông ABCD ta có: $\large SO\perp (ABCD)$
$\large OB=\dfrac{1}{2}BD= \dfrac{\sqrt{2}}{2},\, OM= \dfrac{1}{2}AB= \dfrac{1}{2}$
Xác định $\large 60^\circ = (SB, (ABCD))= (SB, OB)=\widehat {SBO}$ và $\large SO= OB.\tan \widehat{SBO}= \dfrac{\sqrt{6}}{2}$
Gọi M là trung điểm BC, kẻ $\large OK\perp SM$ (1)
Ta có: $\large \left\{\begin{align}& BC\perp OM\\& BC\perp SO\\\end{align}\right.$ $\large \Rightarrow  BC\perp (SOM)\Rightarrow  BC\perp OK$ (2)
Từ (1) và (2) $\large \Rightarrow  OK\perp (SBC)\Rightarrow  d(O, (SBC))= OK$
Tam giác vuông SOM có $\large OK= \dfrac{SO.OM}{\sqrt{SO^2+OM^2}}= \dfrac{\sqrt{42}}{14}$
Vậy $\large d(O, (SBC))= OK= \dfrac{\sqrt{42}}{14}$