Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông tại A c

 Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác ABC vuông tại A có $\large BC= 2a$, $\large AB= a\sqrt{3}$. Khoảng cách từ AA’ đến mặt phẳng (BCC’B’) là: 

• A. $\large \dfrac{a\sqrt{21}}{7}$
• B. $\large \dfrac{a\sqrt{3}}{2}$
• C. $\large \dfrac{a\sqrt{5}}{2}$
• D. $\large \dfrac{a\sqrt{7}}{3}$

Chọn B

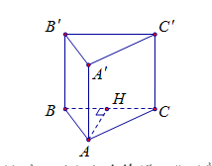
Ta có: $\large AA’// (BCC’B’)$ nên khoảng cách từ AA’ đến mặt phẳng (BCC’B’) cũng chính là khoảng cách từ A đến mặt phẳng (BCC’B’)
Hạ $\large AH\perp BC\Rightarrow  AH\perp (BCC’B’)$
Ta có: $\large \dfrac{1}{AH^2}= \dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{3a^2}+\dfrac{1}{BC^2-AB^2}= \dfrac{1}{3a^2}+\dfrac{1}{a^2}= \dfrac{4}{3a^2}$
$\large \Rightarrow  AH= \dfrac{a\sqrt{3}}{2}$
Vậy khoảng cách từ AA’ đến mặt phẳng (BCC’B’) bằng $\large \dfrac{a\sqrt{3}}{2}$