Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và $\large SA= S

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a và $\large SA= SB= SC= b$. Gọi G là trọng tâm $\large \Delta ABC$. Xét mặt phẳng (P) đi qua A và vuông góc với  SC. Tìm hệ thức liên hệ giữa a và b để (P) cắt SC tại điểm $\large C_1$ nằm giữa S và C

• A. $\large b > a\sqrt{2}$
• B. $\large b < a\sqrt{2}$
• C. $\large a < b\sqrt{2}$
• D. $\large a > b\sqrt{2}$

Chọn C

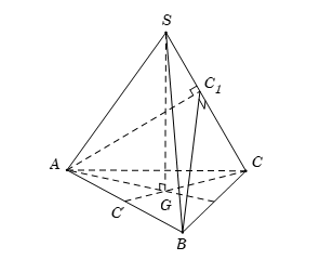
Gọi G là trọng tâm tam giác ABC
Do S. ABC là hình chóp đều nên $\large SG\perp (ABC)$
Gọi C’ là trung điểm AB. Suy ra: C, C’, G thẳng hàng
Ta có: $\large \left\{\begin{align}& AB\perp CC’\\& SG\perp AB\\\end{align}\right. $ $\large \Rightarrow  AB\perp (SCC’)\Rightarrow  AB\perp SC$ (1)
Trong tam giác SAC, kẻ $\large AC_1\perp SC$ (2)
Từ (1) và (2) suy ra: $\large SC\perp (ABC_1)$ 
Suy ra thiết diện cần tìm là tam giác $\large ABC_1$ thỏa mãn đi qua A và vuông góc với SC
Tam giác SAC cân tại S nên để $\large C_1$ nằm giữa S và C khi và chỉ khi $\large \widehat{ASC} < 90^\circ $
Suy ra $\large cos\widehat{ASC} > 0 \Leftrightarrow SA^2+ SC^2- AC^2 > 0 \Leftrightarrow 2b^2- a^2 > 0 \Rightarrow  a < b\sqrt{2}$