Cho hình chóp A. BCD có cạnh $\large AC\perp (BCD)$ và BCD là tam giác

Cho hình chóp A. BCD có cạnh $\large AC\perp (BCD)$ và BCD là tam giác đều cạnh bằng a. Biết $\large AC= a\sqrt{2}$ và M là trung điểm của BD. Khoảng cách từ C đến đường thẳng AM bằng

• A. $\large a\sqrt{\dfrac{2}{3}}$
• B. $\large a\sqrt{\dfrac{6}{11}}$
• C. $\large a\sqrt{\dfrac{7}{5}}$
• D. $\large a\sqrt{\dfrac{4}{7}}$

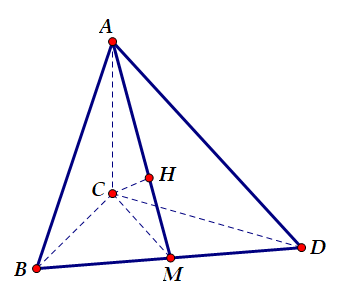
Dựng $\large CH\perp AM\Rightarrow  d(C, AM) = CH$
Vì $\large \Delta BCD$ là tam giác đều cạnh a và M là trung điểm của BD nên dễ tính được $\large CM= \dfrac{a\sqrt{3}}{2}$
Xét $\large \Delta ACM$ vuông tại C có CH là đường cao, ta có:
$\large \dfrac{1}{CH^2}= \dfrac{1}{CA^2}+ \dfrac{1}{CM^2}= \dfrac{1}{2a^2}+ \dfrac{4}{3a^2}= \dfrac{11}{6a^2}$
$\large \Rightarrow  CH^2= \dfrac{6a^2}{11}\Rightarrow  CH= a\sqrt{\dfrac{6}{11}}$