Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a, $\large \wideha

Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a, $\large \widehat{ABC}=60^{0}$. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với mặt phẳng đáy.Tính khoảng cách giữa hai đường thẳng AD và SC, biết góc giữa đường thẳng SD và mặt đáy bằng $\large 60^{0}$

• A. $\large \dfrac{a\sqrt{609}}{19}$
• B. $\large \dfrac{a\sqrt{609}}{29}$
• C. $\large \dfrac{a\sqrt{600}}{20}$
• D. $\large \dfrac{a\sqrt{906}}{29}$

Chọn B

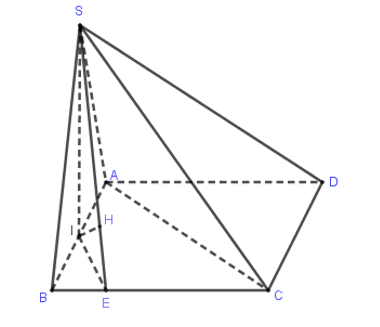
Gọi I là trung điểm AB. Khi đó, ta có: $\large SI\perp (ABCD)$
Do $\large AD//BC$ nên $\large d(AD, SC) = d(AD, (SBC))=d(A, (SBC))= 2d(I, (SBC)) $
Xét $\large \Delta ABD$ có DI là trung tuyến nên $\large DI= \sqrt{\dfrac{DA^2+DB^2}{2}- \dfrac{AB^2}{4}}= \dfrac{a\sqrt{7}}{2}$
Suy ra $\large SI= DI.\tan 60^\circ = \dfrac{a\sqrt{21}}{2}$
Từ I kẻ IE vuông góc với BC. Từ I kẻ IH vuông góc với SE. Khi đó, ta chứng minh được: $\large IH= d(I, (SBC))$
Do I là trung điểm AB trong $\large \Delta ABC$ đều nên $\large IE= \dfrac{1}{2}. \dfrac{a\sqrt{3}}{2}$
Vậy $\large \dfrac{1}{IH^2}= \dfrac{1}{IS^2}+ \dfrac{1}{IE^2}= \dfrac{116}{21a^2}\Rightarrow  IH = \dfrac{\sqrt{609}}{58}$
Kết luận $\large d(AD, SC)= \dfrac{\sqrt{609}}{29}$