Cho hình chóp S.ABC có $\large AB= BC= CA= a,\, SA= SB= SC= a\sqrt{3}$

Cho hình chóp S.ABC có $\large AB= BC= CA= a,\, SA= SB= SC= a\sqrt{3}$, M là điểm bất kì trong không gian. Gọi d là tổng khoảng cách từ M đến tất cả các đường thẳng AB, BC, CA, SA, SB, SC. Giá trị nhỏ nhất của d bằng

• A. $\large 2a\sqrt{3}$
• B. $\large \dfrac{a\sqrt{6}}{2}$
• C. $\large a\sqrt{6}$
• D. $\large \dfrac{a\sqrt{3}}{2}$

Chọn C

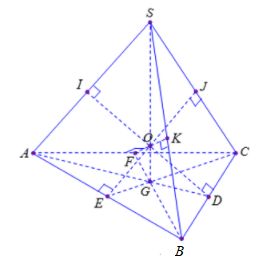
Ta có khối chóp S.ABC là khối chóp tam giác đều
Gọi G là trọng tâm của tam giác ABC. Khi đó SG là chiều cao của khối chóp S.ABC
Gọi D, E, F lần lượt là trung điểm của BC, AB, CA và I, J, K lần lượt là hình chiếu của D, E, F trên SA, SC, SB
Khi đó DI, EJ, FK tương ứng là các đường vuông góc chung của các cặp cạnh SA và BC, SC và AB, SB và CA
Ta có: $\large DI= EJ= FK$. Do đó: $\large \Delta SID= \Delta SJE$ nên $\large SI=SJ$ 
Suy ra $\large ED//IJ$ (cùng song song với AC). Do đó bốn điểm D, E, I, J đồng phẳng
Tương tự ta có bộ bốn điểm D, F, I, K và E, F, J, K đồng phẳng
Ba mặt phẳng (DEIJ), (DFIK), (EFJK) đôi một cắt nhau theo ba giao tuyến DI, EJ, FK. Suy ra: DI, EJ, FK đồng quy tại điểm O thuộc SG
Xét điểm M bất kì trong không gian
Ta có: $\large \left\{\begin{align}& d(M, SA)+d(M, BC)\geq DI\\& d(M, SC)+ d(M, AB)\geq EJ\\& d(M, SB)+d(M, AC)\geq FK\\\end{align}\right.$ $\large \Rightarrow  d\geq DI+ EJ+ FK$ 
Do đó: d nhỏ nhất bằng $\large DI+EJ+FK=3DI$ khi $\large M\equiv O$
Ta có: $\large AD= \dfrac{a\sqrt{3}}{2},\, AG= \dfrac{2}{3}AD=\dfrac{a\sqrt{3}}{3},\, SG= \sqrt{SA^2-AG^2}= \dfrac{2a\sqrt{6}}{3},\, \sin \widehat{SAG}= \dfrac{SG}{SA}= \dfrac{2\sqrt{2}}{3}$ 
Suy ra: $\large DI= AD.\sin \widehat{SAD}= \dfrac{a\sqrt{3}}{2}.\dfrac{2\sqrt{2}}{3}=\dfrac{a\sqrt{6}}{3}$ 
Vậy giá trị cần tìm: $\large 3DI= 3.\dfrac{a\sqrt{6}}{3}=a\sqrt{6}$