Cho hình chóp S.ABCD đáy ABCD là hình thoi tâm O, đường thẳng SO vuông

Cho hình chóp S.ABCD đáy ABCD là hình thoi tâm O, đường thẳng SO vuông góc với mặt phẳng (ABCD). Biết $\large AB=SB=a, SO=\dfrac{a\sqrt{6}}{3}$. Tìm số đo góc giữa hai mặt phẳng (SAB) và (SAD)

• A.

  $\large 30^\circ$

• B.

  $\large 45^\circ$

• C.

  $\large 60^\circ$

• D.

  $\large 90^\circ$

Chọn D

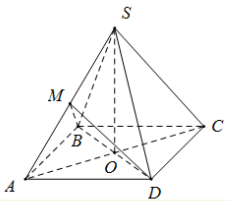
Có $\large SB = AB \Rightarrow SD = AD$

Gọi M là trung điểm SA thì $\large BM\perp SA$ và $\large DM\perp SA$

$\large \Rightarrow $ Góc giữa (SAB) và (SAD) là góc giữa BM và DM

Dễ thấy $\large \Delta BMD$ cân tại M có O là trung điểm BD $\large \Rightarrow MO\perp BD$ 

$\large SO\perp (ABCD)$ nên $\large SO\perp BO\Rightarrow BO=\sqrt{SB^2- SO^2}= \sqrt{a^2-\left(\dfrac{a\sqrt{6}}{3}\right)^2}= \dfrac{a}{\sqrt{3}}$

$\large \Delta OBA=\Delta OBS$ (cạnh huyền - cạnh góc vuông) $\large \Rightarrow OA= OS\Rightarrow \Delta OSA$ vuông cân tại O

$\large \Rightarrow OM= MS= MA= \dfrac{SA}{2}= \dfrac{SO\sqrt{2}}{2}= \dfrac{a}{\sqrt{3}}$

$\large \Rightarrow OM= OB= OD\Rightarrow \Delta BMD$ vuông cân tại M

$\large \Rightarrow $ Góc giữa (SAD) và (SAB) bằng $\large 90^\circ$