Cho hình chóp S.ABC có $\large SA= SB= SC= AB= AC= a,\, BC= a\sqrt{2}$

Cho hình chóp S.ABC có $\large SA= SB= SC= AB= AC= a,\, BC= a\sqrt{2}$. Tính số đo góc (AB, SC) ta được kết quả

• A. $\large 90^\circ $
• B. $\large 30^\circ $
• C. $\large 60^\circ $
• D. $\large 45^\circ $

Chọn C

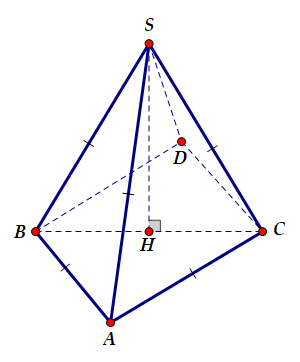
Ta có: $\large AB= AC= a,\, BC= a\sqrt{2}\Rightarrow  AB^2+AC^2=BC^2=2a^2\Rightarrow  \Delta ABC$ vuông cân tại A. 
Gọi H là hình chiếu của S lên (ABC)
Do $\large SA= SB= SC= a$ nên $\large HA= HB= HC\Rightarrow  $ H là trung điểm của BC
Trên mặt (ABC) lấy điểm D sao cho ABDC là hình vuông
Do $\large CD//AB$ nên góc giữa SC và AB cũng bằng góc giữa SC và CD
H là trung điểm của BC nên $\large HC= HD$
Ta có: $\large \Delta SHC= \Delta SHD\Rightarrow  SC= SD= a$
Tam giác SCD có $\large SC= CD= SD= a$ nên là tam giác đều
Do đó $\large \widehat{SCD}= 60^\circ $
Vậy góc giữa SC và AB bằng $\large \widehat{SCD} = 60^\circ $