Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông, $\larg

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông, $\large AB=BC=a,\, A'B= a\sqrt{3}$. Gọi M là trung điểm của cạnh BC. Tính khoảng cách giữa hai đường thẳng AM và B'C

• A. $\large d= \dfrac{a\sqrt{42}}{7}$
• B. $\large d= \dfrac{a\sqrt{21}}{7}$
• C. $\large d= \dfrac{a\sqrt{14}}{7}$
• D. $\large d= \dfrac{a\sqrt{7}}{7}$

Chọn D

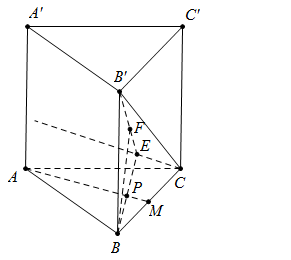
Ta có: $\large AA'=\sqrt{A'B^2- AB^2}=a\sqrt{2}$

Dựng $\large Cx//AM$ khi đó $\large d(AM, B'C)= d(M, (B'Cx))=\dfrac{1}{2}d(B,(B'Cx))$

(vì $\large BM\cap (B'Cx)= C$ và M là trung điểm của BC)

Dựng $\large \left\{\begin{align}& BE\perp Cx\\& BF\perp B'E\\\end{align}\right.$ (1) ta có

$\large \left\{\begin{align}& Cx\perp BE\\& Cx\perp BB'\\\end{align}\right. $ $\large \Rightarrow Cx\perp (BB'E)\Rightarrow Cx\perp BF$ (2)

Từ (1) và (2) suy ra $\large \Rightarrow BF\perp (B'Cx)\Rightarrow d(B, (B'Cx))=BF$

Gọi $\large P=BE\cap AM$, do $\large MP//CE,\, MB=MC$ nên $\large PB= PE$

Mà $\large BP= \dfrac{AB.BM}{\sqrt{AB^2+BM^2}}=\dfrac{a.\dfrac{a}{2}}{\sqrt{a^2+\dfrac{a^2}{4}}}=\dfrac{a}{\sqrt{5}}$

Suy ra: $\large BE=\dfrac{2a}{\sqrt{5}}\Rightarrow BF= \dfrac{BE.BB'}{\sqrt{BE^2+BB'^2}}=\dfrac{2a}{\sqrt{7}}$

Do đó: $\large d(AM,B'C)= \dfrac{a}{\sqrt{7}}$