Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với $\

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D với $\large AB=2a,\, AD=DC=a$. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy. Góc giữa SC và mặt đáy bằng $\large 60^\circ$. Tính khoảng cách d giữa hai đường thẳng AC và SB

• A. $\large d= \dfrac{a\sqrt{6}}{2}$
• B. $\large d= 2a$
• C. $\large d= a\sqrt{2} $
• D. $\large d= \dfrac{2a\sqrt{15}}{5}$

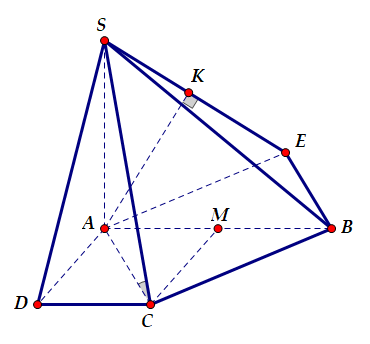
Chọn A

$\large \left\{\begin{align}& (SAB)\perp (ABCD)\\& (SAD)\perp (ABCD)\\& (SAB)\cap  (SAD) = SA\\\end{align}\right.$ $\large \Rightarrow SA\perp (ABCD)$

Xác định $\large 60^0 = (SC, (ABCD)= (SC, AC)= \widehat{SCA}$

và $\large SA=AC.\tan \widehat{SCA}=\sqrt{AD^2+CD^2}.\tan 60^\circ = a\sqrt{2}.\sqrt{3}=a\sqrt{6}$

Gọi M là trung điểm AB, suy ra: ADCM là hình vuông nên $\large CM= AD=a$

Xét tam giác ACB có trung tuyến $\large CM=a=\dfrac{1}{2}AB$ nên tam giác ACB vuông tại C

Lấy điểm E sao cho ACBE là hình chữ nhật nên suy ra: $\large AC//BE$

Do đó: $\large d(AC, SB)= d(AC, (SBE))= d(A, (SBE))$ 

Kẻ $\large AK\perp SE$ (1) ta có $\large \left\{\begin{align}& BE\perp AE\\& BE\perp SA\\\end{align}\right.$ $\large \Rightarrow BE\perp (SAE)\Rightarrow BE\perp AK$ (2)

Từ (1) và (2) suy ra $\large AK\perp (SBE)$

Khi đó: $\large d(A, (SBE))= AK=\dfrac{SA.AE}{\sqrt{SA^2+AE^2}}$

Ta có: $\large AE=BC= \sqrt{a^2+a^2}= a\sqrt{2}\Rightarrow AK=\dfrac{a\sqrt{6}.a\sqrt{2}}{\sqrt{6a^2+2a^2}}= \dfrac{a\sqrt{6}}{2}$