Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và $\large \wideh

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và $\large \widehat{BAD}=60^\circ$. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trọng tâm của tam giác ABC. Góc giữa mặt phẳng (SAB) và (ABCD) bằng $\large 60^\circ$. Khoảng cách từ B đến mặt phẳng (SCD) bằng

• A.

  $\large \dfrac{a\sqrt{21}}{14}$

• B.

  $\large \dfrac{a\sqrt{21}}{7}$

• C.

  $\large \dfrac{3a\sqrt{7}}{14}$

• D.

  $\large \dfrac{3a\sqrt{7}}{7}$

Chọn C

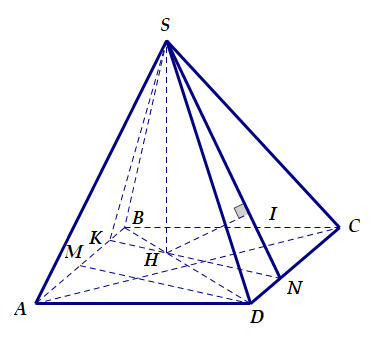
Gọi H là trọng tâm của tam giác ABC, M là trung điểm của AB

Ta có: tam giác ABD đều $\large \Rightarrow DM=\dfrac{a\sqrt{3}}{2}$ và $\large BD=a$

Kẻ $\large HK\perp AB\Rightarrow HK//DM\Rightarrow \dfrac{HK}{DM}=\dfrac{BH}{BD}$

$\large \Rightarrow HK=DM.\dfrac{BH}{BD}=\dfrac{1}{3}.DM=\dfrac{a\sqrt{3}}{6}$

$\large (SAB)\cap (ABCD)=AB,\, AB\perp HK,\, AB\perp SK$ (định lý ba đường vuông góc)

Suy ra $\large (SAB), (ABCD)=(SK,HK)=\widehat{SKH}$

Tam giác SHK vuông tại H có $\large SH=HK.tan 60^0= \dfrac{a}{2}$

Gọi N là giao điểm của HK và CD

Ta có: $\large \left\{\begin{matrix}
HN\perp CD\\ 
SH\perp CD
\end{matrix}\right. \Rightarrow CD\perp (SHN);\, CD\subset (SCD)\Rightarrow (SCD)\perp (SHN)$ và $\large (SHN)\cap (SCD)= SN$

Trong mặt phẳng (SHN) kẻ $\large HI\perp SN$ thì $\large HI\perp (SCD)\Rightarrow HI=d(H, (SCD))$

Tam giác SHN vuông tại H có $\large \dfrac{1}{HI^2}=\dfrac{1}{SH^2}+\dfrac{1}{HN^2}$ với $\large HN=\dfrac{2}{3}DM=\dfrac{a}{\sqrt{3}}\Rightarrow HI=\dfrac{a\sqrt{7}}{7}$

Lại có: $\large \dfrac{BD}{HD}=\dfrac{3}{2}\Rightarrow d(B, (SCD))= \dfrac{3}{2}d(H, (SCD))$

Vậy $\large d(B, (SCD))=\dfrac{3a\sqrt{7}}{14}$