Cho hình chóp S.ABCD, đáy là hình thang vuông tại A và B, biết $\large

Cho hình chóp S.ABCD, đáy là hình thang vuông tại A và B, biết $\large AB= BC= a,\, AD= 2a,\, SA= a\sqrt{3}$ và $\large SA\perp (ABCD)$. Gọi M và N lần lượt là trung điểm của SB, SA. Tính khoảng cách từ M đến (NCD) theo a

• A. $\large \dfrac{a\sqrt{66}}{22}$
• B. $\large 2a\sqrt{66}$
• C. $\large \dfrac{a\sqrt{66}}{11}$
• D. $\large \dfrac{a\sqrt{66}}{44}$

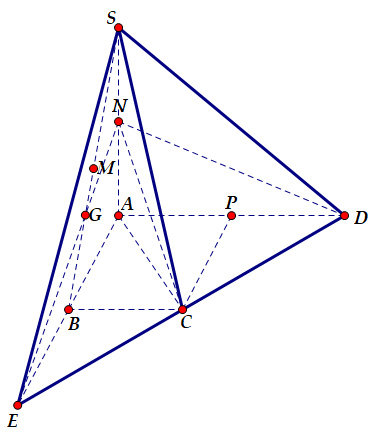
Gọi $\large E= AB\cap CD,\, G= NE\cap SB $
Vì $\large BC//AD,\, BC= \dfrac{1}{2}AD$ nên BC là đường trung bình của tam giác ADE
Do đó: B, C lần lượt là trung điểm của AE, DE
Do đó: G là trọng tâm của tam giác SAE
Kéo theo $\large SG= \dfrac{2}{3}SB$
Mà $\large SM= \dfrac{1}{2}SB$ nên $\large SG= \dfrac{4}{3}SM= \dfrac{4}{3}(SG- MG)\Rightarrow  SG= 4MG$
Do đó: $\large d(S, (NCD))= d(S, (NED))= 4d(M, (NED))\Rightarrow  d(M, (NCD))= \dfrac{1}{4}d(S, (NCD))$
Ta có: $\large S_{AED} = \dfrac{1}{2}AD.AE= \dfrac{1}{2}.2a.2a= 2a^2\Rightarrow  V_{NAED}= \dfrac{1}{3}.NA.S_{AED}= \dfrac{1}{3}. \left( \dfrac{a\sqrt{3}}{2}\right).(2a^2)= \dfrac{a^3\sqrt{3}}{3}$
$\large V_{SAED}= \dfrac{1}{3}.SA.S_{AED}= \dfrac{2a^3\sqrt{3}}{3}\Rightarrow  V_{SNED}= V_{SAED}- V_{NAED}= \dfrac{a^3\sqrt{3}}{3}$
Mặt khác: Gọi P là trung điểm của AD, thì $\large CP\perp AD,\, CP= PD\Rightarrow  \Delta ACD$ vuông tại C
Do đó: $\large CD\perp AC$. Mà $\large CD\perp SA\Rightarrow  CD\perp (SAC)\Rightarrow  CD\perp NC$
Ta có: $\large NC^2= NA^2+AC^2= NA^2+AB^2+BC^2= \dfrac{3a^2}{4}+2a^2= \dfrac{11a^2}{4}$
$\large ED^2= AD^2+AE^2= 8a^2\Rightarrow  S_{NDE}= \dfrac{1}{2}.NC. ED= \dfrac{1}{2}. \left( \dfrac{a\sqrt{11}}{2}\right). \left( 2\sqrt{2}a\right)= \dfrac{a^2\sqrt{22}}{2}$
Vì $\large V_{SNED}= \dfrac{1}{3}d(S, (NED)).S_{NDE}\Rightarrow  d(S, (NED))= \dfrac{3.V_{SNED}}{S_{NDE}}= \dfrac{3. \dfrac{a^3\sqrt{3}}{3}}{\dfrac{a^2\sqrt{22}}{3}}= \dfrac{a\sqrt{66}}{11}$

Vậy $\large d(M, (NCD))=\dfrac{1}{4}.\dfrac{a\sqrt{66}}{11}=\dfrac{a\sqrt{66}}{44}$