Cho hình hộp chữ nhật ABCD.A'B'C'D' có $\large AB=a,\, AD= 2a,\, AA'=

Cho hình hộp chữ nhật ABCD.A'B'C'D' có $\large AB=a,\, AD= 2a,\, AA'= a$. Gọi M là điểm trên đoạn AD với $\large \dfrac{AM}{MD}= 3$. Gọi x là độ dài khoảng cách giữa hai đường thẳng AD', B'C và y là độ dài khoảng cách từ M đến mặt phẳng (AB'C). Tính giá trị xy

• A.

  $\large \dfrac{5a^5}{3}$

• B.

  $\large \dfrac{a^2}{2}$

• C.

  $\large \dfrac{3a^2}{4}$

• D.

  $\large \dfrac{3a^2}{2}$

Chọn B

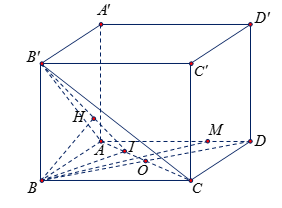
Ta có: $\large B'C//A'D\Rightarrow B'C//(ADD'A')\subset AD'\Rightarrow d(B'C, AD')= d(C, (ADD'A'))= CD= a$

Suy ra: $\large x= a$

Lại có: $\large \dfrac{MA}{DA}= \dfrac{3}{4}\Rightarrow d(M, (AB'C))= \dfrac{3}{4}d(D, (AB'C))= \dfrac{3}{4}d(B, (AB'C))$

Gọi I là hình chiếu vuông góc của B lên AC, ta có: $\large \left\{\begin{matrix}
AC\perp BI\\ 
AC\perp BB'
\end{matrix}\right. \Rightarrow AC\perp (BB'I)$

Gọi H là hình chiếu của B lên B'I ta có:

$\large \left\{\begin{matrix}
BH\perp B'I\\ 
BH\perp AC
\end{matrix}\right. \Rightarrow BH\perp (B'AC)\Rightarrow d(B, ((AB'C))= BH$

Trong tam giác ABC ta có: $\large AB.BC= AC.BI\Rightarrow BI=\dfrac{AB.BC}{AC}= \dfrac{a.2a}{a\sqrt{5}}= \dfrac{2a\sqrt{5}}{5}$

Trong tam giác BB'I ta có: $\large \dfrac{1}{BH^2}= \dfrac{1}{BI^2}+ \dfrac{1}{BB'^2}\Rightarrow BH=\dfrac{BI.B'B}{\sqrt{BI^2+BB'^2}}= \dfrac{2a}{3}$

$\large \Rightarrow d(B, (AB'C))= \dfrac{3}{4}.\dfrac{2a}{3}= \dfrac{a}{2}\Rightarrow y = \dfrac{a}{2}$

Vậy $\large x.y= \dfrac{a^2}{2}$