Cho hình chóp S.ABC có SA, SB, SC tạo với mặt đáy các góc bằng nhau và

Cho hình chóp S.ABC có SA, SB, SC tạo với mặt đáy các góc bằng nhau và bằng $\large 60^\circ $. Biết $\large  BC= a,\, \widehat{BAC}=45^\circ$. Tính $\large h=d(S, (ABC))$

• A.

  $\large h=\dfrac{a\sqrt{6}}{3}$

• B.

  $\large  h = a\sqrt{6}$  

• C.

  $\large  h= \dfrac{a\sqrt{6}}{2}$

• D.

  $\large  h= \dfrac{a}{\sqrt{6}}$

Chọn C

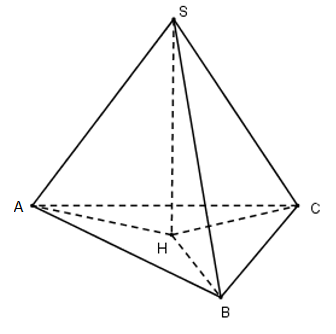
Gọi H là hình chiếu đỉnh S lên mặt phẳng (ABC), khi đó ta có góc tạo bởi SA, SB, AC với đáy lần lượt là $\large \widehat{SAH};\, \widehat{SBH};\, \widehat{SCH}$ và $\large \widehat{SAH}= \widehat{SBH}=\widehat{SCH}= 60^\circ$
Dễ dàng chứng minh được các tam giác vu $\large \Delta SAH=\Delta SBH=\Delta SCH\Rightarrow  HA= HB = HC\Rightarrow  $ H là tâm đường tròn ngoại tiếp tam giác ABC
Đặt $\large SH= h$
Xét tam giác vuông SAH có $\large AH= SH.\cot 60^\circ = \dfrac{h}{\sqrt{3}}= R$
Xét tam giác ABC có: $\large S_{ABC}= \dfrac{AB. AC.BC}{4R}= \dfrac{AB.AC.a}{4\dfrac{h}{\sqrt{3}}}= \dfrac{a\sqrt{3}}{4h}.AB.AC$
Mà $\large S_{ABC}= \dfrac{1}{2}. AB.AC.\sin \widehat{BAC}= \dfrac{1}{2}. \dfrac{\sqrt{2}}{2}. AB.AC= \dfrac{\sqrt{2}}{4}. AB. AC$
$\large \Rightarrow  \dfrac{a\sqrt{3}}{4h}= \dfrac{\sqrt{2}}{4}\Leftrightarrow h=\dfrac{a\sqrt{3}}{\sqrt{2}}= \dfrac{a\sqrt{6}}{2}$