Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A có góc $\large

Cho hình chóp S.ABC có đáy là tam giác ABC vuông tại A có góc $\large \widehat{ABC}= 30^\circ $; tam giác SBC là tam giác đều cạnh a và mặt phẳng $\large (SAB)$ vuông góc mặt phẳng (ABC). Khoảng cách từ A đến mặt phẳng (SBC) là

• A.

  $\large \dfrac{a\sqrt{6}}{5}$

• B.

  $\large \dfrac{a\sqrt{6}}{3}$

• C.

  $\large \dfrac{a\sqrt{3}}{3}$

• D.

  $\large \dfrac{a\sqrt{6}}{6}$

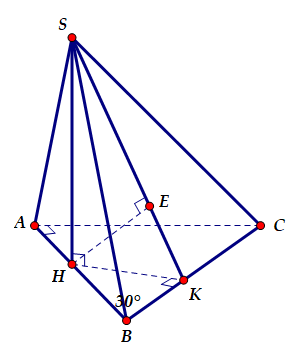
Ta có tam giác ABC vuông tại A có $\large \widehat{ABC}=30^0$ và $\large BC = a$, suy ra $\large AC=\dfrac{a}{2}, AB=\dfrac{a\sqrt{3}}{2}$

Lại có $\large \left\{\begin{matrix}
(SAB)\perp (ABC)\\ 
CA\perp AB
\end{matrix}\right.\Rightarrow AC\perp (SAB)$, suy ra tam giác SAC vuông tại A.

Suy ra $\large SA=\sqrt{SC^2-AC^2}=\sqrt{a^2-\left ( \dfrac{a}{2} \right )^2}=\dfrac{a\sqrt{3}}{2}$

Tam giác SAB có $\large SA=\dfrac{a\sqrt{3}}{2}, AB=\dfrac{a\sqrt{3}}{2}, SB=a$. Sử dụng công thức Hê - rông ta được

$\large S_{SAB}=\dfrac{a^2\sqrt{2}}{4}\Rightarrow SH=\dfrac{2S_{SAB}}{AB}=\dfrac{a\sqrt{6}}{3}\Rightarrow BH=\dfrac{a\sqrt{3}}{3}=\dfrac{2AB}{3}$

Suy ra $\large d\left ( H,(SBC) \right )=\dfrac{2}{3}d\left ( A,(SBC) \right )$

Từ H kẻ $\large HK\perp BC$, kẻ $\large HE\perp SK\Rightarrow HE\perp (SBC)$

Ta dễ tính được $\large HK=\dfrac{a\sqrt{3}}{6}\Rightarrow d(H,(SBC))=\dfrac{a\sqrt{6}}{9}$

Vậy $\large d(A,(SBC))=\dfrac{3}{2}d(H,(SBC))=\dfrac{3}{2}.\dfrac{a\sqrt{6}}{9}=\dfrac{a\sqrt{6}}{6}$