Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, $\large AD= 2AB= 2

Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, $\large AD= 2AB= 2BC= 2CD= 2a$. Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt phẳng (ABCD). Gọi M và N lần lượt là trung điểm của SB và CD. Tính cosin góc giữa MN và (SAC), biết thể tích khối chóp S.ABCD bằng $\large \dfrac{a^3\sqrt{3}}{4}$

• A. $\large \dfrac{\sqrt{310}}{20}$
• B. $\large \dfrac{3\sqrt{5}}{10}$
• C. $\large \dfrac{3\sqrt{310}}{20}$
• D. $\large \dfrac{\sqrt{5}}{10}$

Chọn A

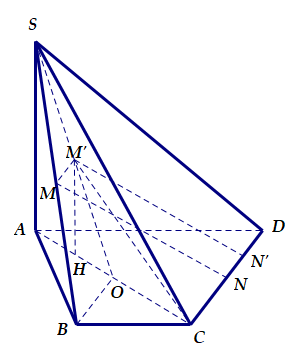
Gọi O là trung điểm của AC 

M', N' lần lượt là trung điểm của SO và ND 

H là trung điểm của AO

Chứng minh được: $\large MN//M'N'$ (vì $\large MM'//BO//NN'$ và $\large MM'=NN'=\dfrac{1}{2}BO$ nên MM'N'N là hình bình hành, do đó $\large MN//M'N'$)

$\large N'C\perp M'C$ (vì $\large AC\perp CD$ và $\large SA\perp CD$ nên $\large CD\perp (SAC)$)

Góc giữa MN và (SAC) là góc giữa M'N' và M'C là $\large \alpha = \widehat{CM'N'}$

Ta có: $\large S_{ABCD}= \dfrac{3a^3\sqrt{3}}{4}\Rightarrow SA= \dfrac{3V_{S.ABCD}}{S_{ABCD}}= a$

$\large M'H= \dfrac{SA}{2}= \dfrac{a}{2};\, CH= \dfrac{3}{4}CA= \dfrac{3a\sqrt{3}}{4}$

$\large M'C= \sqrt{M'H^2+CH^2}= \dfrac{a\sqrt{31}}{4};\, CN'= \dfrac{3}{4}CD= \dfrac{3a}{4}$

$\large M'N'= \sqrt{M'C^2+ CN'^2}=\dfrac{a\sqrt{10}}{2}$

$\large \cos\alpha = \dfrac{M'C}{M'N'}= \dfrac{\sqrt{310}}{20}$