Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuô

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên SA vuông góc với mặt phẳng (ABCD). Đường thẳng SC tạo với mặt phẳng đáy góc $\large 45^\circ $. Khoảng cách giữa hai đường thẳng SB và AC là

• A. $\large d= \dfrac{a\sqrt{10}}{10}$
• B. $\large d= \dfrac{a\sqrt{10}}{2}$
• C. $\large d= \dfrac{a\sqrt{10}}{5}$
• D. $\large d= \dfrac{a\sqrt{10}}{15}$

Chọn C

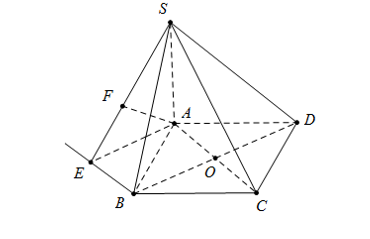
Ta có: $\large AC= a\sqrt{2},\, \angle SCA=\angle (SC, (ABCD))= 45^\circ \Rightarrow  SA= AC= a\sqrt{2} $
Dựng $\large Bx// AC\Rightarrow  d(AC, SB)= d(AC, (SBx))$
Dựng $\large AE\perp Bx,\, AF\perp SE$ (1), ta có:
$\large \left\{\begin{align}& Bx\perp AE\\& Bx\perp SA\\\end{align}\right. $ $\large \Rightarrow  Bx\perp (SAE)\Rightarrow  Bx\perp AF$ (2)
Từ (1) và (2) $\large \Rightarrow  AF\perp (SBE)\Rightarrow  d(SB,AC)= d(AC, (SBx))= d(A, (SBx))= AF$
Ta có: $\large BE// AC\Rightarrow  BE\perp BD$ dễ dàng suy ra: AEBO là hình chữ nhật, suy ra
$\large AE= OB= \dfrac{a\sqrt{2}}{2}$
Vậy $\large d(SB,AC)=  \dfrac{AE.SA}{\sqrt{AE^2+SA^2}}= \dfrac{\dfrac{a\sqrt{2}}{2}.a\sqrt{2}}{\sqrt{\left ( \dfrac{a\sqrt{2}}{2} \right )^2+\left ( a\sqrt{2} \right )^2}}=\dfrac{a\sqrt{10}}{5}$