Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa mặt bê

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa mặt bên và đáy bằng $\large 60^{\circ}$ , diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp tam giác ABC là:

• A.

  A. $\large \dfrac{\pi a^{2}}{4}$

• B.

  B. $\large \dfrac{\pi a^{2}}{6}$

• C.

  C. $\large \dfrac{\pi a^{2}}{3}$

• D.

  D. $\large \dfrac{5\pi a^{2}}{6}$

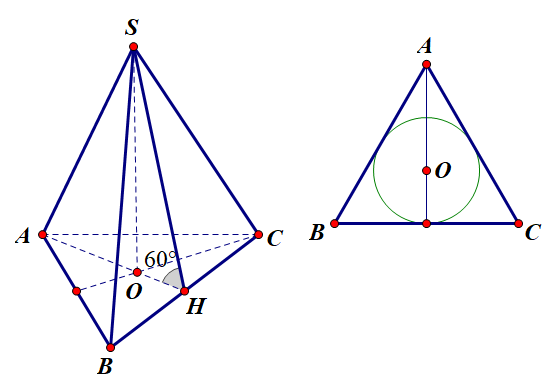
Áp dụng công thức $\large S_{xq} = \pi rl$ với

$\large R = OH = \dfrac{1}{3}AH = \dfrac{1}{3}.\dfrac{a\sqrt{3}}{2} = \dfrac{a\sqrt{3}}{6}$ 

$\large l = SH = \dfrac{OH}{cos60^{\circ}} = \dfrac{\dfrac{a}{2\sqrt{3}}}{\dfrac{1}{2}} = \dfrac{a}{\sqrt{3}}$ 

Vậy $\large S_{xq} = \pi \dfrac{a\sqrt{3}}{6}.\dfrac{a}{\sqrt{3}} = \dfrac{\pi a^{2}}{6}$ 

Vậy chọn đáp án B.