Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng $
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng a√216. Gọi h là chiều cao của khối chóp và R là bán kính mặt cầu ngoại tiếp khối chóp. Tỉ số Rh bằng:
Đáp án án đúng là: C
Lời giải chi tiết:
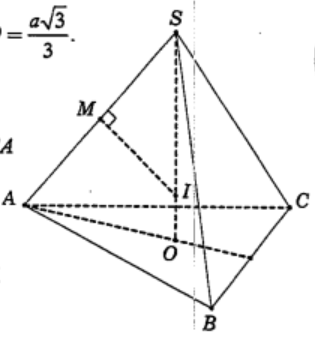
Gọi O là tâm ΔABC, suy ra SO⊥(ABC) và AO=a√33
Trong SOA, ta có h = SO = √SA2−AO2=a2.
Trong mặt phẳng SOA, kẻ trung trực d của đoạn SA cắt SO tại I, suy ra:
I∈d nên IS = IA.
I∈SO nên IA = IB = IC.
Do đó IA = IB = IC = IS nên I là tâm mặt cầu ngoại tiếp khối chóp S.ABC.
Gọi M là trung điểm SA, ta có ΔSMI∼ΔSOA nên
R=SI=SM.SASO=SA22SO=7a12. Vậy Rh=76. Chọn C.
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp S.ABC có đáy ABC là một tam giác đều cạnh bằng a . Cạnh
- Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, $\lar
- Một khối nón có bán kính đáy bằng 2 cm , chiều cao bằng $\large \sqrt{
- Cho hình thang ABCD có ˆA=ˆB=90∘
- Cho khối trụ ( T ), AB và CD lần lượt là hai đường kính trên các mặt đ