Cho hình chóp S.ABC có đáy ABC là một tam giác đều cạnh bằng a . Cạnh

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có đáy ABC là một tam giác đều cạnh bằng a. Cạnh bên $\large SA = a\sqrt{3}$ và vuông góc với đáy (ABC). Bán kính mặt cầu ngoại tiếp khối chóp S.ABC là:
Đáp án án đúng là: C
Lời giải chi tiết:
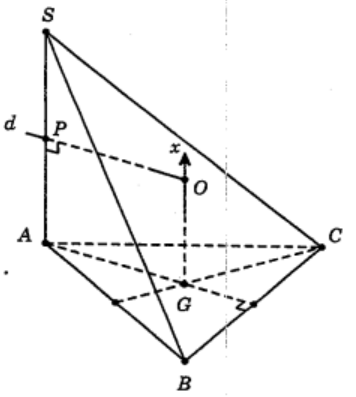
Gọi G là trọng tâm $\large \Delta ABC$, suy ra G là tâm đường tròn ngoại tiếp $\large \Delta ABC$.
Từ G dựng tia $\large Gx \perp (ABC)$ (như hình vẽ).
Suy ra Gx là trục của tam giác ABC.
Trong mặt phẳng (SA, Gx), kẻ trung trực d của đoạn thẳng SA.
Gọi O = $\large Gx \cap d \Rightarrow$ $\large \begin{cases}
& \ O \in Gx \\
& \ O \in d
\end{cases} \Rightarrow \begin{cases}
& \ OA = OB = OC \\
& \ OA = OS
\end{cases}$
$\large \Rightarrow$ OA = OB = OC = OS = R.
Suy ra O là tâm mặt cầu ngoại tiếp khối chóp S.ABC.
Ta có OG = PA = $\large \dfrac{1}{2}SA = \dfrac{a\sqrt{3}}{2}$;
$\large AG = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{a\sqrt{3}}{2} = \dfrac{a\sqrt{3}}{3}$
Trong tam giác vuông OGA, ta có R = OA = $\large \sqrt{OG^{2}+AG^{2}} = \dfrac{a\sqrt{39}}{6}$. Chọn C.
Xem thêm các bài tiếp theo bên dưới
- Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại B, $\lar
- Một khối nón có bán kính đáy bằng 2 cm , chiều cao bằng $\large \sqrt{
- Cho hình thang ABCD có $\large \widehat{A} = \widehat{B} = 90^{\circ}$
- Cho khối trụ ( T ), AB và CD lần lượt là hai đường kính trên các mặt đ
- Cho hình trụ có bán kính đáy R và chiều cao R , lấy hai điểm A, B nằm