Cho hình chóp S.ABCD đáy là hình vuông cạnh a, SA vuông góc với mặt ph

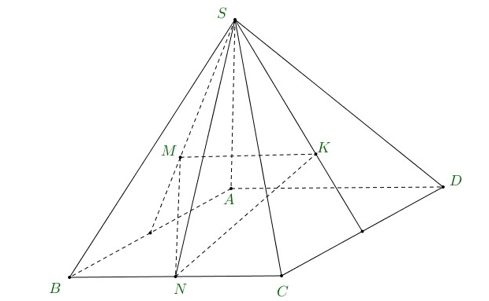
Cho hình chóp S.ABCD đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), SA = a. M, K tương ứng là trọng tâm tam giác SAB, SCD; N là trung điểm BC. Thể tích khối tứ diện SMNK bằng $\large \dfrac {m}{n}.a^{3}$ với $\large m, n \in \mathbb{N},(m, n) = 1$. Giá trị $\large m + n$ bằng

• A.

  28

• B.

  12

• C.

  29

• D.

  32

Ta có: $\large V_{S.ABCD} = \dfrac {1}{3} SA. S_{ABCD} = \dfrac {a^{3}}{3}$
Gọi I là trung điểm của AB, J là trung điểm của CD. Ta có: $\large \Delta SMK$ đồng dạng với $\large \Delta SIJ$ theo tỉ số $\large \dfrac {2}{3}$. Do đó $\large V_{SMNK} =\left(\dfrac {2}{3}\right)^{2} V_{S.NIJ} = \dfrac {4}{9} V_{S.NIJ}$
Mặt khác $\large S_{\Delta NIJ} = \dfrac {1}{4} S_{ABCD}$. Do đó $\large V_{S.NIJ} = \dfrac {a^{3}}{12}$
Nên $\large V_{SMNK} = \dfrac {4}{9} . \dfrac {a^{3}}{12} = \dfrac {a^{3}}{27}$
Vậy m = 1, n = 27. Do đó m + n = 28$