Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng ( ABCD ), tứ giác A

Cho hình chóp S.ABCD có SA vuông góc với mặt phẳng (ABCD), tứ giác ABCD là hình thang vuông với cạnh đáy AD, BC. AD = 3CB = 3a, AB = a, $\large SA = a\sqrt{3}$. Điểm I thỏa mãn $\large \overrightarrow{AD} = 3\overrightarrow{AI}$, M là trung điểm SD, H là giao điểm của AM và SI. Gọi E, F lần lượt là hình chiếu của A lên SB, SC. Tính thể tích V của khối nón có đáy là đường tròn ngoại tiếp tam giác EFH và đỉnh thuộc mặt phẳng (ABCD).

• A.

  A. $\large V = \dfrac{\pi a^{3}}{5\sqrt{5}}$

• B.

  B. $\large V = \dfrac{\pi a^{3}}{2\sqrt{5}}$

• C.

  C. $\large V = \dfrac{\pi a^{3}}{\sqrt{5}}$

• D.

  D. $\large V = \dfrac{\pi a^{3}}{10\sqrt{5}}$

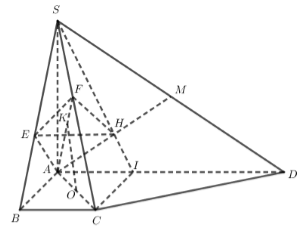
Chọn D

Nhận xét: Tứ giác ABCI là hình vuông. Dễ chứng minh BC $\large \perp$(SAB) và BI $\large \perp$SC.

$\large \left\{\begin{matrix}
EA \perp SB & \\ 
EA \perp BC & 
\end{matrix}\right.\Rightarrow EA \perp(SBC)\Rightarrow EA \perp SC$ 

$\large \left\{\begin{matrix}
EA \perp SC & \\ 
FA \perp SC & 
\end{matrix}\right.\Rightarrow SC \perp(AEF)$ 

Trong tam giác vuông SAB có $\large \dfrac{SE}{SB} = \dfrac{SA^{2}}{SB^{2}} = \dfrac{3}{4}$ 

Trong tam giác SAD có:

$\large \dfrac{HS}{HI}.\dfrac{AI}{AD}.\dfrac{MD}{MS} = 1 \Rightarrow \dfrac{HS}{HI} = 3 \Rightarrow \dfrac{SH}{SI} = \dfrac{3}{4}$ 

Trong tam giác SBI có $\large \dfrac{SE}{SB}=\dfrac{SH}{SI}=\dfrac{3}{4}\Rightarrow EH // BI$ 

Do BI $\large \perp$SC nên EH $\large \perp$SC.

Suy ra các điểm A, E, F, H cùng thuộc mặt phẳng đi qua A và vuông góc với SC.

Gọi K là trung điểm AF.

Vì $\large \left\{\begin{matrix}EA \perp EF & \\ AH \perp FH & \end{matrix}\right. \Rightarrow$ K là tâm đường tròn ngoại tiếp tam giác $\large \Delta EFH$.

Ta có: $\large AF = \dfrac{SA.AC}{SC}=\dfrac{a\sqrt{3}.a\sqrt{2}}{a\sqrt{5}}=\dfrac{a\sqrt{6}}{\sqrt{5}}$ 

Suy ra bán kính đáy của khối nón là $\large R = \dfrac{1}{2}AF = \dfrac{a\sqrt{6}}{2\sqrt{5}}$ 

Gọi O là tâm hình vuông ABCI.

Do $\large \left\{\begin{matrix}
SC \perp (EFH) & \\ 
OK // SC & 
\end{matrix}\right.\Rightarrow OK \perp (EFH)$  $\large \Rightarrow$ O là đỉnh của khối nón.

Chiều cao của khối nón là 

$\large h = \dfrac{1}{2}FC = \dfrac{1}{2}\sqrt{AC^{2}-AF^{2}}=\dfrac{1}{2}\sqrt{2a^{2}-\dfrac{6}{5}a^{2}} = \dfrac{a}{\sqrt{5}}$.

Vậy thể tích khối nón là:

$\large V = \dfrac{1}{3}.\pi R^{2}.h = \dfrac{1}{3}.\pi .\left (\dfrac{a\sqrt{6}}{2\sqrt{5}}  \right )^{2}.\dfrac{a}{\sqrt{5}} = \dfrac{\pi a^{3}}{10\sqrt{5}}$