Cho hình chóp S.ABCD có $\Large S A \perp(A B C D)$, đáy ABCD là hình

Cho hình chóp S.ABCD có $\Large S A \perp(A B C D)$, đáy ABCD là hình chữ nhật có $\Large A B=a \sqrt{3} ; A D=a \sqrt{2}$. Khoảng cách giữa SD và BC.

• A.

  $\Large \dfrac{2 a}{3}$

• B.

  $\Large a \sqrt{3}$

• C.

  $\Large \dfrac{3 a}{4}$

• D.

  $\Large \dfrac{a \sqrt{3}}{2}$

Chọn B

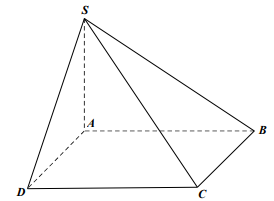
Ta có: $\Large B C //(S A D) \Rightarrow d(S D ; B C)=d(B C ;(S A D))=d(B ;(S A D))=d(C ;(S A D))$

Vì $\Large \left\{\begin{array}{l} A B \perp S A \\ A B \perp A D \end{array} \Rightarrow A B \perp(S A D)\right.$ nên $\Large d(B ;(S A D))=A B=a \sqrt{3}$