Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, $\Large \wideh

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, $\Large \widehat{A B C}=30^{\circ}$. Tam giác SAB đều cạnh a và hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm của cạnh AB . Thể tích khối chóp S.ABC là:

• A. $\Large \dfrac{a^{3} \sqrt{3}}{9}$
• B. $\Large \dfrac{a^{3}}{18}$
• C. $\Large \dfrac{a^{3} \sqrt{3}}{3}$
• D. $\Large \dfrac{a^{3}}{12}$

Chọn D

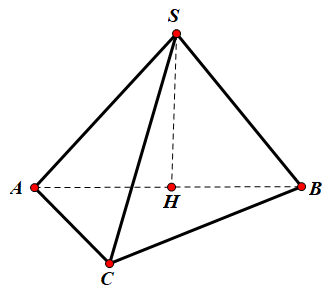
Gọi H là hình chiếu vuông góc của S lên mặt phẳng (ABC) $\Large \Rightarrow$ H là trung điểm cạnh AB

Ta có $\Large S H=\dfrac{a \sqrt{3}}{2}$

Xét tam giác ABC có $\Large A C=A B \cdot \tan \widehat{A B C}=\dfrac{a}{\sqrt{3}}$

$\Large \Rightarrow S_{\Delta A B C}=\dfrac{1}{2} A B \cdot A C=\dfrac{a^{2}}{2 \sqrt{3}}$

Thể tích khối chóp S.ABC là: $\Large V=\dfrac{1}{3} S_{\Delta A B C} \cdot S H=\dfrac{1}{3} \cdot \dfrac{a^{2}}{2 \sqrt{3}} \cdot \dfrac{a \sqrt{3}}{2}=\dfrac{a^{3}}{12}$