Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2√22√2. Cạ
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2√22√2. Cạnh bên SA vuông góc với đáy và SA=3SA=3. Mặt phẳng (α)(α) qua A và vuông góc với SC cắt các cạnh SB, SC, SD tại M, N, P. Tính thể tích mặt cầu ngoại tiếp tứ diện CMNP
Đáp án án đúng là: A
Lời giải chi tiết:
Chọn A
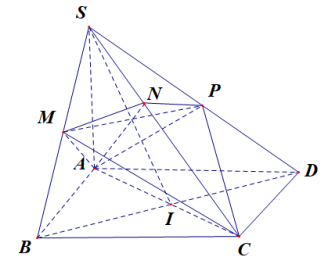
Ta có {SA⊥BCAB⊥BC⇒BC⊥(SAB)⇒BC⊥MA
Lại có MA⊥SC⇒MA⊥(SBC)⇒MA⊥MC(1)
Tương tự: AP⊥PC(2)
Mặt khác AN⊥NC(3)
Gọi I là trung điểm của AC, từ (1), (2) (3) ta có IN=IM=IC=IP(=IA). Mặt cầu ngoại tiếp CMNP là mặt cầu tâm I, bán kính IA.
IA=AC2=√(2√2)2+(2√2)22=2
Thể tích khối cầu ngoại tiếp tứ diện CMNP là: V=43π⋅23=32π3
Xem thêm các bài tiếp theo bên dưới
- Cho phương trình $\Large \log _{2}^{2} x-(5 m+1) \log _{2} x+4 m^{2}+m
- Cho f(x) là hàm số liên tục trên tập xác định R+ và
- Có tất cả bao nhiêu giá trị nguyên của m để hàm số $\Large y=\left|x^{
- Cho y=f(x) là hàm số đa thức bậc 3 và có đồ thị như hình vẽ b
- Cho y=f(x) là hàm đa thức bậc 4 và có đồ thị như hình vẽ. Có