Cho $\Large y=f(x)$ là hàm số đa thức bậc 3 và có đồ thị như hình vẽ b

Cho $\Large y=f(x)$ là hàm số đa thức bậc 3 và có đồ thị như hình vẽ bên. Hỏi phương trình $\Large f(f(\cos x)-1)=0$ có bao nhiêu nghiệm thuộc đoạn $\Large [0 ; 3 \pi]$?

• A. 2
• B. 4
• C. 5
• D. 6

Chọn D

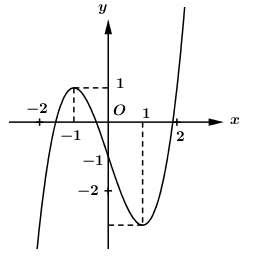
Đặt $\Large t=\cos x$, với $\Large x \in[0 ; 3 \pi] \Rightarrow t \in[-1 ; 1]$

Với $\Large t=1$, phương trình $\Large t=\cos x$ có hai nghiệm $\Large x \in[0 ; 3 \pi]$

Với $\Large t=-1$, phương trình $\Large t=\cos x$ có hai nghiệm $\Large x \in[0 ; 3 \pi]$

Với $\Large -1 < t < 1$, phương trình $\Large t=\cos x$ vào phương trình $\Large f(f(\cos x)-1)=0$, ta được phương trình:

$\Large f(f(t)-1)=0 \Leftrightarrow\left[\begin{array}{l}
f(t)-1=a \in(-2 ;-1) \\
f(t)-1=b \in(-1 ; 0) \\
f(t)-1=c \in(1 ; 2)
\end{array}\right.$ $\Large \Leftrightarrow\left[\begin{array}{l}
f(t)=a+1 \in(-1 ; 0)&(1) \\
f(t)=b+1 \in(0 ; 1) &(2)\\
f(t)=c+1 \in(2 ; 3)&(3)
\end{array}\right.$

Từ đồ thị ta có:

+) Phương trình (1) có 1 nghiệm $\Large t \in(-1 ; 0)$, suy ra phương trình đã cho có 3 nghiệm.

+) Phương trình (2) có 1 nghiệm $\Large t \in(-1 ; 0)$, suy ra phương trình đã cho có 3 nghiệm.

+) Phương trình (3) có 1 nghiệm $\Large t > 1$, suy ra phương trình đã cho vô nghiệm.

Vậy phương trình đã cho có 6 nghiệm.