Cho hai số thục dương x, y thỏa mãn $\Large \log _{2} x+x(x+y)=\log _{

Cho hai số thục dương x, y thỏa mãn $\Large \log _{2} x+x(x+y)=\log _{2}(6-y)+6 x$. Giá trị nhỏ nhất của biểu thức $\Large T=x^{3}+3 y$ là

• A. 16
• B. 18
• C. 12
• D. 20

Chọn A

Điều kiện: $\Large x > 0,0 < y < 6$

Ta có $\Large \log _{2} x+x(x+y)=\log _{2}(6-y)+6 x$ $\Large \Leftrightarrow \log _{2} x+x^{2}=\log _{2}(6-y)+6 x-x y$

$\Large \Leftrightarrow \log _{2} x+\log _{2} x+x^{2}=\log _{2}(6-y)+\log _{2} x+6 x-x y$

$\Large \Leftrightarrow \log _{2}\left(x^{2}\right)+x^{2}=\log _{2}[x(6-y)]+x(6-y)\quad (*)$

Xét hàm số $\Large f(t)=\log _{2} t+t$ trên $\Large (0 ;+\infty)$

Ta có $\Large f^{\prime}(t)=\dfrac{1}{t \cdot \ln 2}+1 > 0, \forall t \in(0 ;+\infty)$ nên hàm số f(t) đồng biến trên $\Large (0 ;+\infty)$

Khi đó $\Large (*) \Leftrightarrow f\left(x^{2}\right)=f(x(6-y)) \Leftrightarrow x^{2}=x(6-y)$$\Large \Leftrightarrow x=6-y \Leftrightarrow y=6-x$

$\Large \Rightarrow T=x^{3}+3(6-x)=x^{3}-3 x+18=g(x)$

Xét hàm số $\Large g(x)=x^{3}-3 x+18$ trên $\Large (0 ;+\infty)$

Ta có $\Large g^{\prime}(x)=3 x^{2}-3 ; g^{\prime}(x)=0 \Leftrightarrow\left[\begin{array}{l}
x=-1 \notin(0 ;+\infty) \\
x=1 \in(0 ;+\infty)
\end{array}\right.$

Bảng biến thiên

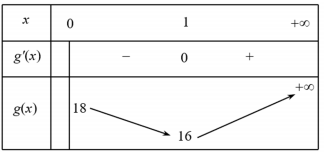
Từ bảng biến thiên suy ra $\Large T=g(x) \geq g(1)=16$. Dấu "=" xảy ra khi và chỉ khi $\Large \left\{\begin{array}{l}
x=1 \\
y=6-x=5
\end{array}\right.$