Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O, cạnh a. G

Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O, cạnh a. Gọi M, N lần lượt là trung điểm của SA và BC. Góc giữa đường thẳng MN và mặt phẳng (ABCD) bằng $\Large 60^\circ$. Tính cos của góc giữa đường thẳng MN và mặt phẳng (SBD).

• A.

  $\Large \dfrac{\sqrt{41}}{4}$

• B.

  $\Large \dfrac{\sqrt{5}}{5}$

• C.

  $\Large \dfrac{2 \sqrt{5}}{5}$

• D.

  $\Large \dfrac{2 \sqrt{41}}{4}$

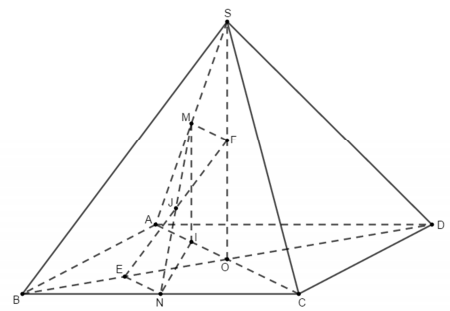
Từ giả thiết ta có $\Large S O \perp(A B C D)$

Gọi I là trung điểm OA thì MI là đường trung bình của $\Large \Delta S O A \Rightarrow M I / / S O \Rightarrow M I \perp(A B C D)$

$\Large \Rightarrow$ I là hình chiếu của M trên mặt phẳng (ABCD) $\Large \Rightarrow$ IN là hình chiếu của MN  trên mặt phẳng (ABCD). Suy ra $\Large (\widehat{M N,(A B C D)})=(\widehat{M N, I N}) \Rightarrow \widehat{M N I}=60^{\circ}$

Ta có $\Large N C=\dfrac{1}{2} B C=\dfrac{a}{2} ; I C=\dfrac{3}{4} A C=\dfrac{3 a \sqrt{2}}{4}$

Áp dụng định lý cosin trong $\Large \Delta INC$ ta có $\Large I N^{2}=C I^{2}+C N^{2}-2 C I . C N \cdot \cos \widehat{N C I}$

$\Large \Rightarrow I N^{2}=\left(\dfrac{3 a \sqrt{2}}{4}\right)^{2}+\left(\dfrac{a}{2}\right)^{2}-2 \cdot \dfrac{3 a \sqrt{2}}{4} \cdot \dfrac{a}{2} \cdot \cos 45^{\circ}=\dfrac{5 a^{2}}{8} \Rightarrow I N=\dfrac{a \sqrt{10}}{4}$

Do $\Large \Delta MIN$ vuông tại I nên $\Large \cos \widehat{M N I}=\dfrac{I N}{M N} \Rightarrow M N=\dfrac{I N}{\cos 60^{\circ}}=\dfrac{a \sqrt{10}}{4}: \dfrac{1}{2}=\dfrac{a \sqrt{10}}{2}$

Lại có $\Large A C \perp B D, A C \perp S O \Rightarrow A C \perp(S B D)$

Gọi E là trung điểm OB $\Large \Rightarrow$ EN là đường trung bình của $\Large \Delta B O C \Rightarrow E N / / O C$ hay $\Large E N / / A C$

$\Large \Rightarrow N E \perp(S B D)$ hay E là hình chiếu của N trên mặt phẳng (SBD)

Gọi F là trung điểm của SO $\Large \Rightarrow$ MF là đường trung bình của $\Large \Delta S A O \Rightarrow M F / / A O$ hay $\Large MF / / AC$

$\Large \Rightarrow M F \perp(S B D)$ hay F là hình chiếu của M trên mặt phẳng (SBD).

Ta có $\Large M F / / N E$ nên bốn điểm E, N, F, M cùng nằm trên một mặt phẳng

Trong mặt phẳng (ENFM) gọi $\Large J=M N \cap E F \Rightarrow J=M N \cap(S B D)$ (do $\Large E F \subset(S B D)$)

Suy ra $\Large (\widehat{M N,(S B D)})=(\widehat{M N, E F})=\widehat{E J N}$ (do $\Large \widehat{E J N} < 90^{\circ}$)

Ta có $\Large E N=\dfrac{1}{2} O C=\dfrac{1}{4} A C=\dfrac{a \sqrt{2}}{4}$; $\Large M F=\dfrac{1}{2} A O=\dfrac{1}{4} A C=\dfrac{a \sqrt{2}}{4} \Rightarrow E N=M F$, mà $\Large EN //MF$

$\Large \Rightarrow$ Tứ giác ENFM là hình bình hành $\Large \Rightarrow$ I là trung điểm $\Large M N \Rightarrow J N=\dfrac{1}{2} M N=\dfrac{a \sqrt{10}}{4}$

Vậy $\Large \cos (\widehat{M N,(S B D)})=\cos \widehat{E J N}=\dfrac{J E}{J N}=\dfrac{\sqrt{J N^{2}-E N^{2}}}{J N}$$\Large =\dfrac{\sqrt{\left(\dfrac{a \sqrt{10}}{4}\right)^{2}-\left(\dfrac{a \sqrt{2}}{4}\right)^{2}}}{\dfrac{a \sqrt{10}}{4}}=\dfrac{2 \sqrt{5}}{5}$