Cho hình lăng trị ABC.A'B'C' có đáy ABC là tam giác vuông tại A, cạnh

Cho hình lăng trị ABC.A'B'C' có đáy ABC là tam giác vuông tại A, cạnh $\Large B C=2 a$ và $\Large \widehat{A B C}=60^{\circ}$. biết tứ giác BCC'B' là hình thoi có $\Large \widehat{B^{\prime} B C}$ nhọn. Mặt phẳng (BCC'B') vuông góc với (ABC) và mặt phẳn (ABB'A') tạo với (ABC) góc $\Large 45^\circ$. Thể tích khối lăng trụ ABC.A'B'C' bằng

• A. $\Large \dfrac{\sqrt{7} a^{3}}{7}$
• B. $\Large \dfrac{3 \sqrt{7} a^{3}}{7}$
• C. $\Large \dfrac{6 \sqrt{7} a^{3}}{7}$
• D. $\Large \dfrac{\sqrt{7} a^{3}}{21}$

Chọn B

Có $\Large \left\{\begin{array}{l}
\left(B C C^{\prime} B^{\prime}\right) \perp(A B C) \\
\left(B C C^{\prime} B^{\prime}\right) \cap(A B C)=B C
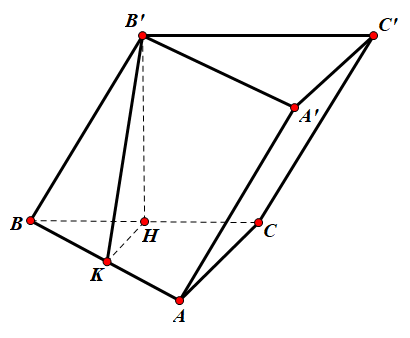
\end{array}\right.$. Do đó trong (BCC'B') kẻ B'H vuông  góc với BC tại H thì $\Large B^{\prime} H \perp(A B C)$ hay B'H là chiều cao của hình lăng trụ

Trong (ABC) kẻ HK vuông góc với AB tại K. Khi đó $\Large AB \perp\left(B^{\prime} H K\right)$

Ta có $\Large \left\{\begin{array}{l}
\left(A B B^{\prime} A^{\prime}\right) \cap(A B C)=A B \\
\left(B^{\prime} H K\right) \perp A B\right. \\
\left(B^{\prime} H K\right) \cap\left(A B B^{\prime} A^{\prime}\right)=B^{\prime} K,\left(B^{\prime} H K\right) \cap(A B C)=K H
\end{array}\right.$

$\Large \Rightarrow$ Góc giữa (ABB'A') và (ABC) chính là góc giữa B'K và KH

$\Large \Delta B^{\prime} H K$ vuông tại H nên $\Large \widehat{B^{\prime} K H}$ là góc nhọn. Do đó $\Large \widehat{B^{\prime} K H}=45^{\circ}$

$\Large \Delta B^{\prime} H K$ vuông tại H có $\Large \widehat{B^{\prime} K H}=45^{\circ} \Rightarrow \Delta B^{\prime} H K$ vuông cân tại $\Large H \Rightarrow B^{\prime} H=K H$

Xét hai tam giác vuông B'BH và BKH, ta có $\Large \tan \widehat{B^{\prime} B H}=\dfrac{B^{\prime} H}{B H}=\dfrac{K H}{B H}=\sin \widehat{A B C}=\sin 60^{\circ}=\dfrac{\sqrt{3}}{2}$

$\Large \Rightarrow \dfrac{B^{\prime} H}{B^{\prime} B}=\sin \widehat{B^{\prime} B H}=\sqrt{1-\cos ^{2} \widehat{B^{\prime} B H}}$ $\Large \left.=\sqrt{1-\left(\dfrac{1}{\tan ^{2} \widehat{B^{\prime} B H}+1}\right.}\right)=\sqrt{1-\dfrac{1}{\dfrac{3}{4}+1}}=\dfrac{\sqrt{21}}{7}$

$\Large \Rightarrow B^{\prime} H=B^{\prime} B \cdot \dfrac{\sqrt{21}}{7}=\dfrac{2 a \sqrt{21}}{7}$ (vì BCC'B'  là hình thoi có cạnh $\Large BC=2a$)

Ta có $\Large S_{A B C}=\dfrac{1}{2} A B \cdot A C=\dfrac{1}{2}\left(B C \cdot \cos 60^{\circ}\right)\left(B C \cdot \sin 60^{\circ}\right)$$\Large =\dfrac{1}{2} \cdot 2 a \cdot \dfrac{1}{2} \cdot 2 a \cdot \dfrac{\sqrt{3}}{2}=\dfrac{a^{2} \sqrt{3}}{2}$

Vậy $\Large V_{A B C . A^{\prime} B^{\prime} C^{\prime}}=B^{\prime} H . S_{A B C}=\dfrac{2 a \sqrt{21}}{7} \cdot \dfrac{a^{2} \sqrt{3}}{2}=\dfrac{3 \sqrt{7} a^{3}}{7}$