Cho $\Large y=f(x)$ là hàm đa thức bậc 4 và có đồ thị như hình vẽ. Có

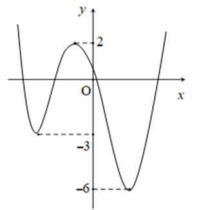
Cho $\Large y=f(x)$ là hàm đa thức bậc 4 và có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-12;12] để hàm số $\Large g(x)=|2 f(x-1)+m|$ có 5 điểm cực trị?

• A. 13
• B. 14
• C. 15
• D. 12

Chọn C

Đặt $\Large h(x)=2 f(x-1)+m \Rightarrow g(x)=|h(x)|$

Số điểm cực trị của $\Large g(x) =$ số điểm cực trị của $\Large y=h(x)+$ số giao điểm của $\Large y=h(x)$ với trục Ox khác với điểm cực trị của $\Large y=h(x)$

Hàm só $\Large y=f(x)$ có 3 điểm cực trị. Suy ra hàm số $\Large y=h(x)$ cũng có 3 điểm cực trị

Hàm số $\Large g(x)$ có 5 điểm cực trị khi và chỉ khi $\Large h(x)=0 \Leftrightarrow f(x-1)=-\dfrac{m}{2}$ có 2 nghiệm phân biệt khác điểm cực trị của $\Large h(x)$

Đồ thị hàm số $\Large y=f(x-1)$ có được bằng cách tịnh tiến đồ thị hàm số $\Large y=f(x)$ sang bên phải 1 đơn vị

Dựa vào đồ thị, ta đươc: $\Large -\dfrac{m}{2} \geq 2$ hoặc $\Large -6 < -\dfrac{m}{2} \leq-3$

$\Large \Leftrightarrow\left[\begin{array}{l}
m \leq-4 \\
6 \leq m < 12
\end{array} \stackrel{m \in Z ; m \in[-12 ; 12]}{\longrightarrow}\right.$ có 15 giá trị m nguyên thỏa mãn yêu cầu bài toán