Cho f(x) là hàm số liên tục trên tập xác định R+ và
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
Cho f(x) là hàm số liên tục trên tập xác định R+ và thỏa mãn f(x2+3x+1)=x+2. Tính I=∫51f(x)dx
Đáp án án đúng là: C
Lời giải chi tiết:
Chọn C
f(x2+3x+1)=x+2
⇔(2x+3)f(x2+3x+1)=(2x+3)(x+2)
⇔∫10(2x+3)f(x2+3x+1)dx=∫10(2x+3)(x+2)dx=616
Đặt t=x2+3x+1⇒dt=(2x+3)dx
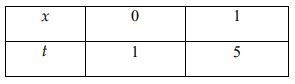
Suy ra ∫51f(t)dt=616
Xem thêm các bài tiếp theo bên dưới
- Có tất cả bao nhiêu giá trị nguyên của m để hàm số $\Large y=\left|x^{
- Cho y=f(x) là hàm số đa thức bậc 3 và có đồ thị như hình vẽ b
- Cho y=f(x) là hàm đa thức bậc 4 và có đồ thị như hình vẽ. Có
- Cho hình lăng trị ABC.A'B'C' có đáy ABC là tam giác vuông tại A, cạnh
- Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông tâm O, cạnh a. G