Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB là tam

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, tam giác SAB là tam giác vuông cân tại đỉnh S, và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng 

• A. $\large \dfrac{a^3\sqrt{2}}{2}$
• B. $\large \dfrac{a^3}{2}$
• C. $\large \dfrac{a^3\sqrt{2}}{6}$
• D. $\large \dfrac{a^3}{6}$

Chọn D

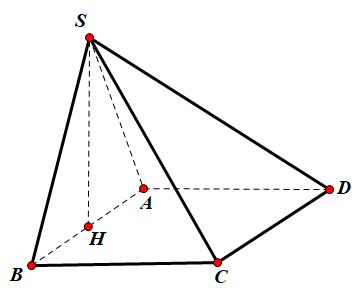
Gọi H là trung điểm của AB, ta có: 

$\large \left\{\begin{align}& (SAB)\perp (ABCD)\\& (SAB)\cap (ABCD)= AB\\& SH\perp AB\\\end{align}\right. $

Suy ra: $\large SH\perp (ABCD)$

Diện tích hình vuông ABCD là: $\large S_{ABCD}= a^2$

Do tam giác SAB vuông cân tại S nên $\large SH = \dfrac{AB}{2} = \dfrac{a}{2}$

Thể tích khối chóp S.ABCD có chiều cao $\large SH = \dfrac{a}{2}$ và diện tích đáy $\large S_{ABCD}= a^2$ là: 

$\large V= \dfrac{1}{3}.S_{ABCD}.SH= \dfrac{1}{3}.a^2.\dfrac{a}{2} = \dfrac{a^3}{6}$