Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a. Hình chiếu vuông gó

Cho hình chóp S.ABCD có đáy là hình vuông cạnh 3a. Hình chiếu vuông góc của S trên mặt phẳng đáy ABCD là điểm H thuộc cạnh AB sao cho HB=2HA. Cạnh SA hợp với mặt phẳng đáy góc $\Large 60^\circ$. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABCD

• A. $\Large 21 \pi a^{2}$
• B. $\Large \dfrac{55 \pi a^{2}}{3}$
• C. $\Large \dfrac{475 \pi a^{2}}{3}$
• D. $\Large 22 \pi a^{2}$

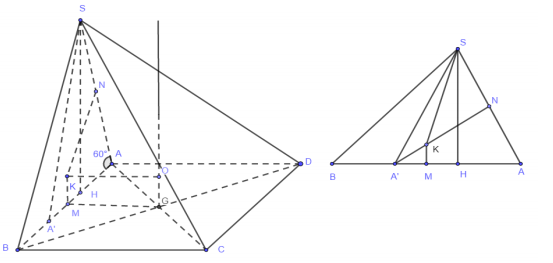
Gọi G là tâm hình vuông ABCD ; M , N lần lượt là trung điểm AB, SA; A' là điểm đối xứng của A qua H .

Vì A' là điểm đối xứng của A qua H nên ta có HA=HA'. Suy ra SH là đường trung trực của AA'. Do đó $\Large \Delta SAA'$ là tam giác cân.

Mà $\Large \widehat{S A A^{\prime}}=(\widehat{S A,(A B C D)})=60^{\circ}$. Do đó $\Large \Delta SAA'$ là tam giác đều cạnh bằng 2a.

Từ M kẻ đường trung trực của AB cắt A'N tại K. Khi đó K là tâm đường tròn ngoại tiếp $\Large \Delta SAB$

Qua G dựng trục đường tròn ngoại tiếp Gy của hình vuông ABCD.

Qua K dựng trục đường tròn ngoại tiếp Kx của $\Large \Delta SAB$.

Gọi $\Large O=K x \cap G y$ là tâm mặt cầu ngoại tiếp hình chóp S.ABCD

Ta có $\Large A^{\prime} N=\sqrt{A A^{\prime 2}-A N^{2}}=a \sqrt{3} ; M A^{\prime}=\dfrac{a}{2}$

Ta lại có $\Large \Delta M K A^{\prime} \sim \Delta N A A^{\prime} \Rightarrow \dfrac{A^{\prime} K}{A A^{\prime}}=\dfrac{M A^{\prime}}{N A^{\prime}}=\dfrac{\dfrac{a}{2}}{a \sqrt{3}}=\dfrac{\sqrt{3}}{6}$ $\Large \Rightarrow A^{\prime} K=\dfrac{\sqrt{3}}{6} A A^{\prime}=\dfrac{a \sqrt{3}}{3}$

$\Large \Rightarrow K N=A^{\prime} N-A^{\prime} K=\dfrac{2 a \sqrt{3}}{3}$

Mặt khác $\Large K O=M G=\dfrac{A D}{2}=\dfrac{3 a}{2}$

Khi đó bán kính mặt cầu ngoại tiếp $\Large R^{2}=S O^{2}=K S^{2}+K O^{2}=\dfrac{55 a^{2}}{12}$

Vậy diện tích mặt cầu ngoại tiếp là $\Large \dfrac{55 \pi a^{2}}{3}$