Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, $\Large S

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, $\Large S A \perp(A B C D), A D=3 a$, $\Large S A=A B=B C=a$. Gọi S' là điểm thỏa mãn $\Large \overrightarrow{S S^{\prime}}=\dfrac{1}{2} \overrightarrow{A B}$. Tính thể tích khối đa diện SS'ABCD.

• A.

  $\Large \dfrac{13 a^{3}}{10}$

• B.

  $\Large \dfrac{11 a^{3}}{12}$

• C.

  $\Large \dfrac{11 a^{3}}{10}$

• D.

  $\Large \dfrac{13 a^{3}}{12}$

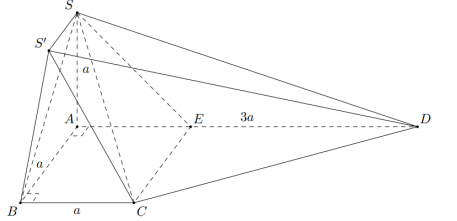
Gọi E là điểm trên cạnh AD sao cho $\Large DE=2AE$

Do $\Large \overrightarrow{S S^{\prime}}=\dfrac{1}{2} \overrightarrow{A B} \Rightarrow S S^{\prime}=\dfrac{a}{2}$

Ta có: $\Large \left\{\begin{array}{l} B C \perp A B \\ B C \perp S A \end{array} \Rightarrow B C \perp\left(S A B S^{\prime}\right)\right.$

$\Large V_{S S^{\prime} A B C D}=V_{S . A B C D}+V_{C B S S'}+V_{D . C S S'}$

Trong đó:

+) $\Large V_{S . A B C D}=\dfrac{1}{3} S_{A B C D} \cdot S A=\dfrac{1}{3} \cdot \dfrac{1}{2} \cdot(B C+A D) \cdot A B \cdot S A=\dfrac{1}{6} \cdot(a+3 a) \cdot a \cdot a=\dfrac{2 a^{3}}{3}(đvtt)$

+) $\Large V_{C . B S S^{'}}=\dfrac{1}{3} S_{B S S^{\prime}} C B=\dfrac{1}{3} \cdot \dfrac{1}{2} \cdot S S^{\prime} \cdot d\left(B, S S^{\prime}\right) \cdot C B=\dfrac{1}{6} \cdot S S^{\prime} \cdot S A . C B=\dfrac{1}{6} \cdot \dfrac{a}{2} \cdot a \cdot a=\dfrac{a^{3}}{12}( đvtt )$

+) Do $\Large d\left(D,\left(C S S^{\prime}\right)\right)=2 d\left(A,\left(C S S^{\prime}\right)\right)$ nên suy ra

$\Large V_{D . CSS^{'}}=2 V_{A.C S S^{\prime}}=2 V_{C.{A S S'}}=2 \cdot \dfrac{1}{3} S_{A S S^{'}} . C B$$\Large =\dfrac{2}{3} \cdot \dfrac{1}{2} S A \cdot S S^{\prime} \cdot C B=\dfrac{1}{3} a \cdot \dfrac{a}{2} \cdot a=\dfrac{a^{3}}{6}( đvtt )$

Vậy $\Large V_{S S^{\prime} A B C D}=\dfrac{2 a^{3}}{3}+\dfrac{a^{3}}{12}+\dfrac{a^{3}}{6}=\dfrac{11 a^{3}}{12} \quad( đvtt )$